データサイエンス
Data Science
データサイエンス(Data Science)とは、データそのものの性質やデータを取り扱う手法を研究する科学全般を指す言葉で、統計学、機械学習、データマイニング、可視化・・など、様々な分野を包括する概念です。
数値や文字(カテゴリ)として得られるデータを統計的手法や機械学習(近年の AI の技術ベース)などを用いて分析・処理することによって、世界に潜む様々な物事の関係(モデル)を見出す科学であるとも言えます。
関連する諸分野との関係を図で表すと、以下のようになります。
GoogleImage:Data Science Machine Learning AI
CONTENTS
- はじめに
- データサイエンス序説
- 関数について
- 説明変数と目的変数
-
データサイエンスの手法
- 概要
- データの取得
- データの読み込み|ReadData
- 可視化|Data Visualization
- 線形回帰|Linear Regression
- ロジスティック回帰|Logistic Regression
- サポートベクターマシン|Support Vector Machine(SVM)
- 決定木|Decision Tree
- ランダムフォレスト|Random Forest
- ニューラルネットワーク|Neural Network(NN)
- 主成分分析|Principal Component Analysis(PCA)
- k-means法|k-means Clustering
- 付記:機械学習とデータマイニング
- 付記:クラス分類とクラスタリング
- プログラムの開発環境
- Python ライブラリ
- データライブラリ
- APPENDIX
はじめに
データ至上主義の限界
データサイエンスは「x は A のグループに属する」とか「AよりもBの方が売り上げに貢献する」、「x は1年後にCに達するだろう」といった判別や予測を「既存の(過去の)データをもとに行う」もので、収集するデータが多くなれば、人間の経験に基づく「直感」よりもその精度が高くなることは確かです。
しかし、それをそのまま未来のデザインに適用してよいか・・という話になると、そこにはいくつかの配慮が必要になります。
例えば、採用面接で Aさん、Bさんのどちらを採用するか・・という選択に関して考えてみましょう。使う単語、話し方、視線の動き・・それらと採用後の業績をリンクした大量のデータがあれば、人事担当者の直感よりも AIの判定の方が正確に対象を見極めるかもしれません(ちなみに「筆記試験の点数で人を選ぶ」というのも、データで人を見ているわけですから、実質的には同じです)。しかし、その先が問題です。「あなたはAIの判定(筆記試験の点数)によって当社に採用されました」と言われるのと、「社長が『あなたが必要だ』と言ったので採用されました」と言われるのとでは、あなた自身のセルフイメージ(自己像)に違いが生まれ、入社後のモチベーションも変わるのではないでしょうか。人間というのは「生産完成品」ではありません。「誰かに必要とされている」という自意識は、それ以後の人を大きく変えるのです。AIによる判定(予測)が有効なのは、対象が「生産完成品(所与のもの)」である場合に限られます。
また例えば、A,B どちらの商品企画を実際に採用するか・・については、別の視点が必要です。人間はそもそも「未だ見たこともないもの」に欲望を抱くことができません。革命的な新商品というものは、そもそも「過去のニーズ」から生まれたものではなく、それが世に登場することによって「新たなニーズを生み出す」ものと言えます。AIによる判定(予測)が正しく機能するのは、対象が既存のニーズの枠組みを出ないものである場合に限られます。
要するに、データというものは参考にはなりますが、そればかりに注力しても、組織のパフォーマンスもあがらず、イノベーションも起きない・・ということです。データサイエンスとの付き合い方を間違えない・・ということが重要です。
データサイエンス序説
モデルを見出すこと
データサイエンスの最大の関心事は、物事の背景にある「関係(モデル)」を探ることです。それは科学全般に言えることですが、従来のように科学者の経験的な直感によってその仮説が生まれるのではなく、あくまでも、現実世界にあるデータからそれを数学的に導き出すということがデータサイエンスの特徴です。
「気温が上がると、商品Aの売上が上がる」、「こういう動作をする人物は、商品を盗む可能性が高い」、「身長が高い人は、体重も大きい」など、私たちのまわりには「ああすればこうなる(因果)」「ああであればこうである(相関)」という形でその関係をモデル化して説明できることがたくさんあります。
「アクセルを踏み込むとスピードが上がる」のように、操作すればすぐわかる関係もあるし、「気温上昇と商品Aの売上上昇」のように、気づくのに時間がかかるものもあります。いずれにせよ、人間の脳は、何度か同じような経験をする(複数のデータをとる)ことで、「ああすればこうなるんじゃないか」とか「ああいうときはこうなんじゃないか」という法則を直感的に見出すわけです。
BigDataの活用
しかし、人間の感覚・知覚や記憶力には限界があります。事項間の心理的な距離がありすぎてその関係に気づかない・・そんな法則がたくさん潜んでいる可能性があります。ここに登場したのが、大量のデータ(Big Data)から関係・ルールを見出すデータサイエンスの技術です。発想そのものは昔からあったものですが、近年のコンピュータの計算速度の飛躍的な向上、メモリーサイズの増大がそれをようやく可能にしました。
例えば、あるスーパーマーケットにおいて一定期間中の商品の売上データを全部使うと、「商品Aの売上と商品Xの売上が連動している」というような、人間では気づかないような相関関係が見つかることがあります。データから物事の背後にある仕組みを見出すことができれば、これを使って未来におこることを「予測」することができます。「商品Aを特売する日には、同時に商品Xの在庫も増やしておく・・」といった戦略が立てられるということです。
発見された連動関係を未来に利用するかどうかを決めるのは人間ですが、人間が気づかなかった参考情報が提供されるという点で、データサイエンスは、良くも悪くも、これからの社会の「意思決定」に大きな影響を与える存在となったといえるでしょう。
データサイエンスにできること
- 判別:情報の判断・仕分け・検索、音声・画像の認識、異常検知など
- 予測:数値予測、ニーズ・意図予測、マッチングなど
- 実行:作業の自動化、表現生成、行動の最適化など
関数について
関数の式
関数とは「入力と出力(ああすればこうなる)」の関係を表したモデルです。
y = f ( x )
教科書に出てくる関数の式ですね。ここで嫌になる方もいるかもしれませんが、もう少しお付き合いください。関数 f を一次の関係式と仮定すると、
y = ax +b
と書くことができます。この「a, b によって特徴づけられた、入力x と 出力y の関係」というものが、物事の背景にある原理、未来を予測するためのモデル・・ということになります。
数学の教科書であれば・・
2つの点 (2,5) , (4,9) を通る直線の式を y = ax + b として、 a ,b の値を求めよ・・みたいな問題で、
5 = 2a + b 9 = 4a + b
これを解いて、a = 2, b =1 ( 直線の式は y = 2x + 1)が答えです。
ここまでだと全然面白くないのですが、では「 x = 10 のときに y はいくつ?」という問いになると( 2 x 10 + 1 = 21 )、これがいわば「未来予測」で、少しは役に立ちそうな話になってきます。
しかし、現実的ではありません。
実際の問題になると・・
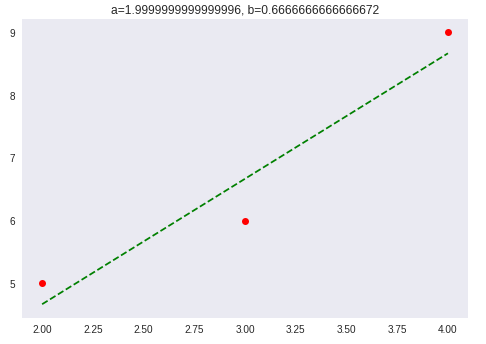
数学の問題というのは、与えられるデータの数も値も、手計算で綺麗な解が導けるように与えられますが、実際の問題では、与えられるデータは必ずしも綺麗に直線上には並びません。例えば (2,5) , (3,6) , (4,9) だったりします。
y = ax + b という直線的な関係を前提とした場合、データが2件であれば連立方程式を解いて a,b の解が求まりますが、3つ以上になると「解なし」つまり、普通の数学の問題としては回答不能になります。
しかし、実際に複数のデータをグラフにプロットすると、明らかに比例関係が見てとれます(右上グラフ)。であれば、その関係を表現するための aとb を見出すことには意味があると言えるでしょう。
現実世界から得られるデータには様々な誤差が含まれていたり、他の要因が影響していたりして、その値はブレるのが普通です。手計算で綺麗に解けるものなどありません。
そこで実際には、最小二乗法という回帰分析の手法を使ってパラメータ a,bを推定するのですが*1、結果からいうと、上記の3つのデータから推定されるのは、a=2.0, b=0.67 となります。もし、入力(x)が 16 であると想定すると、予測値(y)は、32.67 となります。
データサイエンスがやろうとしていることは、基本的にこの応用です。関数モデルをつくって「前提(x)がこうなら、結果(y)はこうなる」といったようなことを予測できるようにしたいわけです。
実際の現象は非常に複雑で、要因(変数)が多数ある(x0, x1, x2, x3, ・・・)だけでなく、それらが重層的に絡みあいます。この関数は非常に複雑なものになるので、関数の形を現実の予測に役立つようにするには過去の経験データも大量に必要になります。
プログラム例
上記の計算を実際に行うプログラムの例を以下に掲載しています。
ipynb(JupyterNotebook)形式で、GitHubに置いていますが、レンダリングがタイムアウトする場合は、下の nbviewer 経由でご覧下さい。
- GitHub:LeastSquaresMethod.ipynb
- nbviewer:LeastSquaresMethod.ipynb
説明変数と目的変数
データサイエンスでは、入力と出力、原因と結果など、2つの変数を「説明変数と目的変数」のような言葉で明確に区別します。
関数モデルを y = f(X) と書いた場合の、X が説明変数で、y が目的変数です*2。
説明変数:explanatory variable
物事の原因となる変数。一般に x を使います。文献によっていろんな表現がありますが、以下、ほぼ同じ意味で使用されています。
- 特徴量 feature / attribute
- データ data
- 予測変数 predictor variable
- 独立変数 independent variable
- 入力 input
目的変数:target variable
物事の結果(予測)となる変数。一般に y を使います。文献によっていろんな表現がありますが、以下、ほぼ同じ意味で使用されています。
- ラベル label
- ターゲット target
- 応答変数 response variable
- 従属変数 dependent variable
- 出力 output
付記
各種記事では X vs Y の組み合わせは以下のパターンが多いようです。
- 説明変数 vs 目的変数
- 特徴量 vs ラベル
- データ vs ターゲット scikit-learn ではこの表現
- 予測変数 vs 応答変数
- 独立変数 vs 従属変数
- 入力 vs 出力
データサイエンスの手法
概要
まずは、様々な手法を分類した事例です。
- 教師あり学習
- 分類
- 回帰
- 教師なし学習
- クラスタリング
- 次元圧縮
- 強化学習
- 機器制御
- 戦略の構築(囲碁・将棋など)
- その他
- 推薦(Recommend) 教師あり、教師なし
- 異常検知 教師あり、半教師あり、教師なし
- 文章・音声・画像の生成
- 同、変換
データの取得
データサイエンスの学習や実践には、大量のデータが必要になります。自身でサンプルデータを作る、アンケートフォーム等を用いてデータを回収するなどの方法もありますが、政府機関等から一般公開されているオープンデータの利用や、Web上の情報を回収する方法なども有効です。以下、参考ページです。
データの読み込み|ReadData
統計処理を行うには、.csv や .xlsx などのデータファイルを読み込む作業が必要です。以下、参考ページです。
- 通常の Python環境で作業する場合 > Pandas
- GoogleColaboratory で作業する場合 > GoogleColaboratory
可視化|Data Visualization
可視化とは、物事の関係性を視覚的に捉えられるように、データを画像・グラフ・図表などに変換することを言います。代表的なのは「散布図」です。
線形回帰|Linear Regression
- 線形回帰は、説明変数 X と目的変数 y との間にある関係を求める、つまり y = f(X) となる関数 f を求める 教師あり・回帰 の代表的な手法です。
ロジスティック回帰|Logistic Regression
- ロジスティック回帰とは、線形回帰分析を分類問題に応用したアルゴリズムで、例えば、商品を購入するか否か、衝突するか否か、採用すべきか否かなどの2値分類を、0から1の範囲の確率を示すロジスティック関数を用いて推測します。
- 詳細:LogisticRegression(準備中)
サポートベクターマシン|Support Vector Machine(SVM)
サポートベクターマシンは 教師あり・分類 の手法の一つで、グループ間のマージン(余白)を最大化するという発想でデータを分類する手法です。与えられたデータが線形分離可能ではない場合は、カーネル法を併用して、データを高次元の特徴空間上へ写像するかたちで分類します。
GoogleImage:サポートベクターマシン カーネル法
- 詳細:SupportVectorMachine(準備中)
決定木|Decision Tree
決定木は、対象がどのカテゴリー(名義尺度)に属するかを予測する 教師あり・分類 の手法の一つで、条件分岐によってグループを分割します。意志決定の参考となる情報を得るためのグラフとなるもので、文字どおり、幹から枝葉へと向かう樹木のような有向グラフになります。
- 詳細:DecisionTree
ランダムフォレスト|Random Forest
条件分岐をもった幾つかの決定木をランダムに構築して、それらの結果を組み合わせて、「分類」または「回帰」を行う多数決的な手法です。決定木の集合体を用いた「アンサンブル学習」と言われます。
- 詳細:RandomForest(準備中)
ニューラルネットワーク|Neural Network(NN)
ニューラルネットワークは、教師あり・クラス分類 の代表的な手法のひとつで、今話題のディープラーニングはその応用にあたります。
主成分分析|Principal Component Analysis(PCA)
主成分分析とは教師なし・次元削減の手法のひとつで、多数の説明変数を、少数の合成変数(複数の変数が合体したもの)に要約する手法です。
k-means法|k-means Clustering
k-means法は、教師なし・クラスタリングの代表的な手法のひとつで、サンプルをグループ分けする目的で使用します。
- 詳細:k-means
付記:機械学習とデータマイニング
これまで紹介してきたいくつかの事例は、 機械学習や データマイニングという言葉と深い関係があります。
機械学習とは、大量のデータを利用した反復的な学習によって情報処理モデルを作成する手法のことで、一方、データマイニングとは、大量のデータから役立つ可能性のある未知の知見を抽出する発見的(heuristic)な手法のことです。
両者の目的の違いから言うと、機械学習の主目的が、入力データを「既知」の特徴と照合させる(「教師あり」で訓練する)ことにあるのに対し、データマイニングの目的は、データから「未知」の特徴を発見する(「教師なし」)ことにある・・というふうに、説明することができます。応用先という視点で言えば、機械学習の(今話題の)応用先は主に AIシステム。データマイニングの応用先は新たなビジネス・・ということができます。
付記:クラス分類とクラスタリング
この2つは、言葉は似ていますが、全く異なることを目指しています。
- クラス分類:対象を既存のグループに振り分ける問題(正解がある)
例:手書きの数字を認識させる|「教師あり」の学習 - クラスタリング:特徴の違うグループを見出す問題(絶対的な正解はない)
例:顧客のグルーピング|「教師なし」の学習
プログラムの開発環境
Google Colaboratory
Google Colaboratory は、Googleアカウントさえあれば、 Jupyter Notebook(python)を用いた環境ですぐに学習をスタートさせることができる点、また個人のPCではハードルが高い GPU環境を使うことができる点で注目を集めています。
- 記事を独立させました。> GoogleColaboratory
Jupyter Notebook
IPython(Pythonを対話的に実行するためのシェル)と WebUI を組み合わせて、ブラウザから利用できる環境です。
- Python :汎用プログラミング環境
- IPython :Pythonを対話的に実行するためのシェル
- Jupyter Notebook:対話型プログラミング環境
- Anaconda :仮想環境の使い分けが簡単な統合環境
- Anaconda > Jupyter Notebook(Python)
- Anaconda > Spyder(Python)
- Anaconda > R-Studio(R)
Orange
Orange は汎用のデータサイエンスツールで、スロベニア Ljubljana 大学のコンピューター情報サイエンス学部で開発が始まり、現在ではオープンソースとしてコミュニティベースで開発が続けられています。
- Orange:データフロープログラミング環境
http://orange.biolab.si
Python ライブラリ
いくつかの定番ライブラリを紹介します。
Pandas|データ解析用ライブラリ(BSD)
Pandas は、データの読込、集計、並べ替え、欠損値の補完などを行うことができるライブラリで、データ分析の前処理段階で多く利用されます。.csv、.xlsx 他、多様な形式のデータを読み込みに対応しています。
データ分析の過程では、Pandasでデータを整形した後、NumPyで数値計算を行う・・といった流れになります。
Pandas の特徴は DataFrame にあります。DataFrame にはデータの平均値や行数などの情報把握、並替え、列名変更といったデータ整形機能があります。
- 記事を独立させました > Pandas
NumPy|行列演算等の数値計算モジュール(修正BSD)
NumPy は、数値計算や行列演算を行うライブラリで、浮動小数点型の行列演算を高速に行える他、三角関数や平方根などの数値計算機能も豊富です。
NumPy は、データの前処理の終了後、整形済みデータに対して数値計算を行う際に利用されます。
SciPy|NumPyベースの数値解析(New BSD)
SciPyは、NumPy(配列オブジェクトとその他の基本的な機能を備えた )を基礎としたライブラリで、統計、最適化、積分、線形代数、フーリエ変換、信号・イメージ処理、遺伝的アルゴリズム、ODE (常微分方程式) ソルバ、特殊関数、その他のモジュールを提供します。
Matplotlib|グラフ描画ライブラリ(BSD)
Matplotlibは、Pythonの代表的なグラフ描画ライブラリで、2D・3Dを含めた多種類のグラフを描画することができます。Pandas、NumPy などと組み合わせてデータの概要把握やデータの特徴の可視化に、データ分析の様々な段階で使用されます。
seaborn|ビジュアライゼーションライブラリ(BSD)
seabornとは、matplotlibをベースにしたグラフ描画ライブラリで、matplotlibよりも美しいグラフを簡単に描画できます。公式サイトによると、その特徴は・・
- matplotlibのデフォルトよりも美しいグラフテーマ群
- データのパターンを明らかにする美しいプロットのためのカラー選択ツール
- データのサブセット間の分布を可視化するための関数群
- 複数種類のデータの線形回帰と可視化ツール群
- 時系列データの状態推定と誤差推定の関数
- グリット状の複雑なグラフを簡単に描画するシステム
pillow|画像処理
https://pillow.readthedocs.io/en/stable/
リサイズやトリミングなどの基本的な処理を行う画像処理ライブラリです。Pythonには、画像認識など高度な画像処理を行う OpenCV というライブラリもありますが、NumPy との連携(画像をNumPyの配列ndarrayとして読み込む)により、画素値ごとの算術演算が可能になります。
- 記事を独立させました > Pillow
scikit-learn|定番機械学習ライブラリ(BSD)
http://scikit-learn.org/stable/
scikit-learn (サイキット・ラーン)は Python用のオープンソース (BSD ライセンス) の機械学習ライブラリで、NumPy, SciPy や Matplotlib と互換性を持つように開発されています。データの前処理、分類、回帰、クラスタリングなど、機械学習のアルゴリズムを幅広く実装しています。
分類(クラス分類)向きのものと、回帰(予測)向きのもの、計7つの定番データサンプルも同梱されています。
- 記事を独立させました > scikit-learn
TensorFlow|機械学習用ライブラリ(Apache License 2.0 by Google)
TensorFlowとは、Google がオープンソースとして開発・公開している、機械学習のためのソフトウェアライブラリで、Python 他いくつかの言語に対応しています。特に深層学習(ディープラーニング)向きのライブラリです。
TensorBoardと呼ばれる視覚化のためのツールが含まれていて、TensorFlowグラフを視覚化したり、画像等のデータを表示することもできます。
Tensor(テンソル)とは線形的な量を表す概念を一般化したもので、多次元の配列として表現できるます。テンソル ≡ 多次元配列 と考えて良いでしょう。
Keras|ニューラルネットワークライブラリ(MIT)
Kerasは、オープンソースのニューラルネットワークライブラリで、TensorFlow他の様々なライブラリの上部で動作します。標準的なニューラルネットワークに加えて、畳み込みニューラルネットワークと回帰型ニューラルネットワークをサポートしています。
データライブラリ
データサイエンスの学習には、プログラムの動作を試すのにサンプルデータが必要になります。よく用いられる統計データサンプルを紹介します。
なお、R や Orange には、はじめからデータサンプルが同梱されていて、その中には、以下で紹介する著名なデータセットも含まれています。
統計用データリポジトリ
- Open Data 一般
> ページを独立させました。OpenData
- 朱鷺の杜(ときのもり)Wiki|DataSet
http://ibisforest.org/index.php?DataSet
- UCI Machine Learning Repository
カリフォルニア大学アーバイン校が運営する、機械学習やデータマイニングに関するデータの配布サイトです。
http://archive.ics.uci.edu/ml/index.html
- Kaggle|The Home of Data Science & Machine Learning
世界中の機械学習・データサイエンスに携わる人が集まるコミニティー
https://www.kaggle.com/
- AWS パブリックデータセット
Amazon AWSが公開する誰でも無料で利用可能なパブリックデータセット。衛星写真、ゲノムデータ、ニュースのモニタリングデータなど、様々なデータが公開されています。
https://registry.opendata.aws/
以下、個別のデータセットで著名なものの一例です。
iris.csv
irisデータとは、英国の植物学者ロナルド・フィッシャー氏が 1936年の論文に発表した多変量データです。 Iris setosa、Iris virginica、Iris versicolor という3種類のアイリス(あやめ)について、それぞれ 50サンプルずつ集めた、計150件のデータからなるデータセットで、変数は、がく片の長さ、がく片の幅、花びら長さ、花びらの幅(単位はいずれも cm)の4つです。
以下、様々なURLから、そのデータを取得することができます。また Python のライブラリにも付属しているので、回帰分析や多変量解析など、様々な事例学習にサンプルとして利用できます。
- http://archive.ics.uci.edu/ml/datasets/Iris
- https://raw.githubusercontent.com/uiuc-cse/data-fa14/gh-pages/data/iris.csv
- https://ja.osdn.net/frs/g_redir.php?m=kent&f=irisdss%2FIRIS.csv
The Boston Housing Dataset
ボストンの物件の価格と、物件の人口統計に関する情報。
解説記事の多さから、紹介していますが、このデータは倫理的な理由により、サンプルとしての利用を控える傾向にあります。今後は カリフォルニア住宅価格データセットの利用が推奨されています。
CRIM・・・犯罪発生率(人口単位)
ZN・・・25,000平方フィート以上の住宅区画の割合
INDUS・・・非小売業の土地面積の割合(人口単位)
CHAS・・・チャールズ川沿いかどうか(1:Yes、0:No)
NOX・・・窒素酸化物の濃度(pphm単位)
RM・・・1戸あたりの平均部屋数
AGE・・・1940年よりも前に建てられた家屋の割合
DIS・・・ボストンの主な5つの雇用圏までの重み付きの郷里
RAD・・・幹線道路へのアクセス指数
TAX・・・10,000ドルあたりの所得税率
PTRATIO・・・教師あたりの生徒の数(人口単位)
B・・・アフリカ系アメリカ人居住者の割合(人口単位)
LSTAT(%)・・・低所得者の割合
MEDV・・・ 所有者が住んでいる住宅価格の中央値(単位 $1000's)
- https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
- https://raw.githubusercontent.com/selva86/datasets/master/BostonHousing.csv
Wine Quality
ポルトガルワインの一種であるヴィーニョ・ヴェルデ(Vinho Verde)を測定したデータで、データセットは赤ワインと白ワインの2種類のデータ群からなります。ワイン(銘柄不明)ごとに測定された13種類の成分データとそのワインの味を評価したグレード(数値)がわかります(グレードは3人以上のワイン査定士が評価した結果の中間値で、「0:とてもまずい」 から 「10:絶品」まで。
Alcohol・・・アルコール
Malic acid・・・リンゴ酸
Ash・・・灰
Alcalinity of ash・・・灰のアルカリ性
Magnesium・・・マグネシウム
Total phenols・・・フェノール類全量
Flavanoids・・・フラバノイド
Nonflavanoid phenols・・・非フラバノイドフェノール類
Proanthocyanins・・・プロアントシアニン
Color intensity・・・色彩強度
Hue・・・色調
OD280/OD315 of diluted wines・・・蒸留ワインのOD280/OD315
Proline・・・プロリン
THE MNIST DATABASE
手書き文字のサンプルデータ配布サイト。MNIST(エムニスト)は、手書きの数字画像セットで、28 x 28 ピクセル、0 (白) ~ 255 (黒) の値からなる画像が計70,000枚。そのうち60,000枚はトレーニングセットで10,000枚はテストセット。画像認識のサンプルとして有名です。
http://yann.lecun.com/exdb/mnist/
MegaFace and MF2
約70万人分の顔写真(同一人につき複数画像)が用意されています。顔認証の機械学習のサンプルに使えます。
APPENDIX
関連ページ
- Data
- Statistics
- DataVisualization
- MachineLearning
- DataMining
- ArtificialIntelligence
- ArtificialIntelligence/Links