正規分布とベキ分布
Normal Distribution / Power-law Distribution
正規分布|Normal Distribution
概要
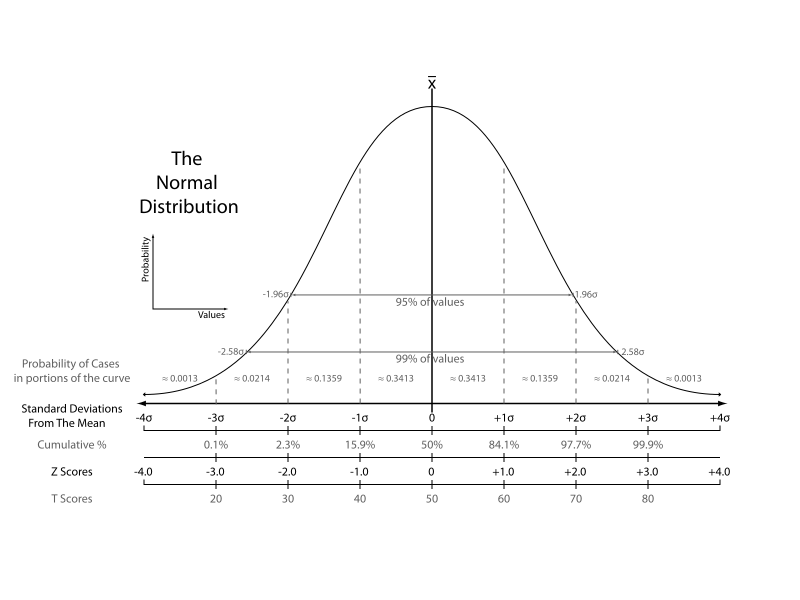
正規分布とは、身長、体重、成績などの分布グラフでよく見かける、平均値を中心とした左右対称な山型の分布で「ベルカーブ」とも呼ばれます。自然界の現象から人間の行動まで、あらゆる現象によく当てはまる標準的な確率分布です。天文観測データの測定誤差がある法則に従うことを数学者C.F.ガウスが見出した経緯もあって「ガウス分布」とも呼ばれます。
グラフの出典:Wikimedia Commons
確率密度関数
この分布を表す関数式は一般に確率密度関数と呼ばれるもので、定義域全区間で積分すると 1.0 になります。
- 正規分布:
\(N( μ, σ^2 )\)
( μ:平均、σ:標準偏差)
\[f(x) = \frac{1}{\sqrt{2πσ^2}} e^{ -\frac{(x-μ)^2}{2σ^2} }\]
- 標準正規分布:
\(N( 0, 1 )\)
確率変数 X の線形変換 \(Z = \frac{X−μ}{σ}\) は 標準正規分布:N(0,1) に従います。\[f(z) = \frac{1}{\sqrt{2π}} e^{ -\frac{z^2}{2} }\]
特徴
正規分布は、ランダムな動きをするものの統計的な分布です。正規分布は統計の基礎として、特に経済学で数学モデルを作る際に前提とされてきました。
- 平均値と最頻値と中央値が一致する
- 平均値を中心にして左右対称になる( 平均 μ に関して左右対称)
- x軸が漸近線になる
- 分散(散らばり)が大きくなると山は低く、逆に分散が小さくなると山は高く尖った形になる
事例
- 身長、体重、血圧、血糖値、成績・・・・
- 偏差値
- 平均 μ、標準偏差を σ とすると、データ
\(x\)
の 偏差値は以下で求まります。
\[\frac{( x - μ ) }{σ} \times 10 + 50\]
- 平均 μ の位置が偏差値 50 です。
- 平均 μ より σ だけ右の位置が偏差値 60になります。
- 平均 μ、標準偏差を σ とすると、データ
\(x\)
の 偏差値は以下で求まります。
- IQも偏差値と同様の考え方で、こちらは平均が 100 です
偏差値 20 30 40 50 60 70 80 IQ 55 70 85 100 115 130 145
- 95% of values:- 1.96σ 〜 + 1.96σ
- データがこの範囲に入る確率が全体の 95%
- 人は一般に 「20人に1人」つまり 5% 程度の確率でしか生起しない現象に対して「めったに起こらないことが起こった」と感じます。仮説検定で使用される有意水準 α の値としては、この 5% がよく用いられます
- 99% of values:- 2.58σ 〜 + 2.58σ
- データがこの範囲に入る確率が全体の 99%
- 統計的検定において厳密さが求められる自然科学では、有意水準 α の値として 1% がよく用いられます
ベキ分布|Power-law Distribution
概要
ベキ分布とは、右図のようなベキ乗則(Power Law)に従う分布です。統計で用いる分布モデルといえば、正規分布がふつうですが、世の中には実は、それとはまったく性質の異なる分布となる現象が多いことが知られています。1890年代にイタリアのパレート(80:20の法則)は収入分布の研究中にこれを発見しました。また、アメリカのグーテンベルクとリヒターは1950年代に地震の大きさと頻度の研究中に、それがベキ乗則に従っていることを発見しました。近年では、ネットワークの研究でもその性質に注目が集まっています。
From Wikimedia Commons
ベキ分布の数式
特徴
ベキ分布の特徴は、分布が左右対称になる正規分布とは対照的に、中央値・最頻値が分布の左端に位置します。平均や分散という概念が事実上意味をなさないという点で、正規分布とは異質なものになります。
ベキ分布はどの尺度で拡大・縮小しても、常に同じような分布になるという「スケールの不変性」があります。
この世界には、正規分布よりも、ベキ分布に従う事例が多く存在します。例えば、重力やクーロン力のような自然現象に見られる逆二乗則、ITの分野では、ロングテールという言葉で語られる現象もそうです。これらの現象では、極端な値をとるサンプルの数が正規分布より多く、そのため大きな値の方向に向かって曲線は長くなだらかに伸びます。
例えば商品売り上げのグラフを、縦軸・販売数量(population)、横軸・商品名(product)として販売数量順に並べると、あまり売れない商品が「恐竜の尻尾」のように伸びます。一般に「商品の売り上げの上位の20%が全体の80%を占める」という「パレートの法則」を説明する現象で、世の中には販売数量が低い商品のアイテム数が圧倒的に多いことを物語ります。
事例
近年の経済物理学の研究から、下記のような事象は、正規分布とは明らかに異なる形、即ちベキ分布に従っている・・と考えられるようになりました。
- 自然現象:ガラスを床に落としたときの破片の大きさの分布、地震の大きさと発生頻度、山火事の被害面積ごとの発生頻度・・
- 経済現象:商品の売上分布、株価、為替等の市場価格の変動、所得分布、純資産の分布・・
著名な現象・法則
- 地震の大きさに関するグーテンベルグ・リヒター則
- 収入の分布に関するパレートの法則
- 構造的自己相似性(フラクタル)
- 生物学的体系におけるスケーリング法則(アロメトリー)
- スケールフリーネットワーク
事例 ネットワークにおけるベキ分布
同様の現象は、ネットワークにおいても顕著に見られます。
- 人々の友人関係の数をみると、一部の人は非常に多くの友人を持つが、大多数の人々は友人の数はごく限られている。
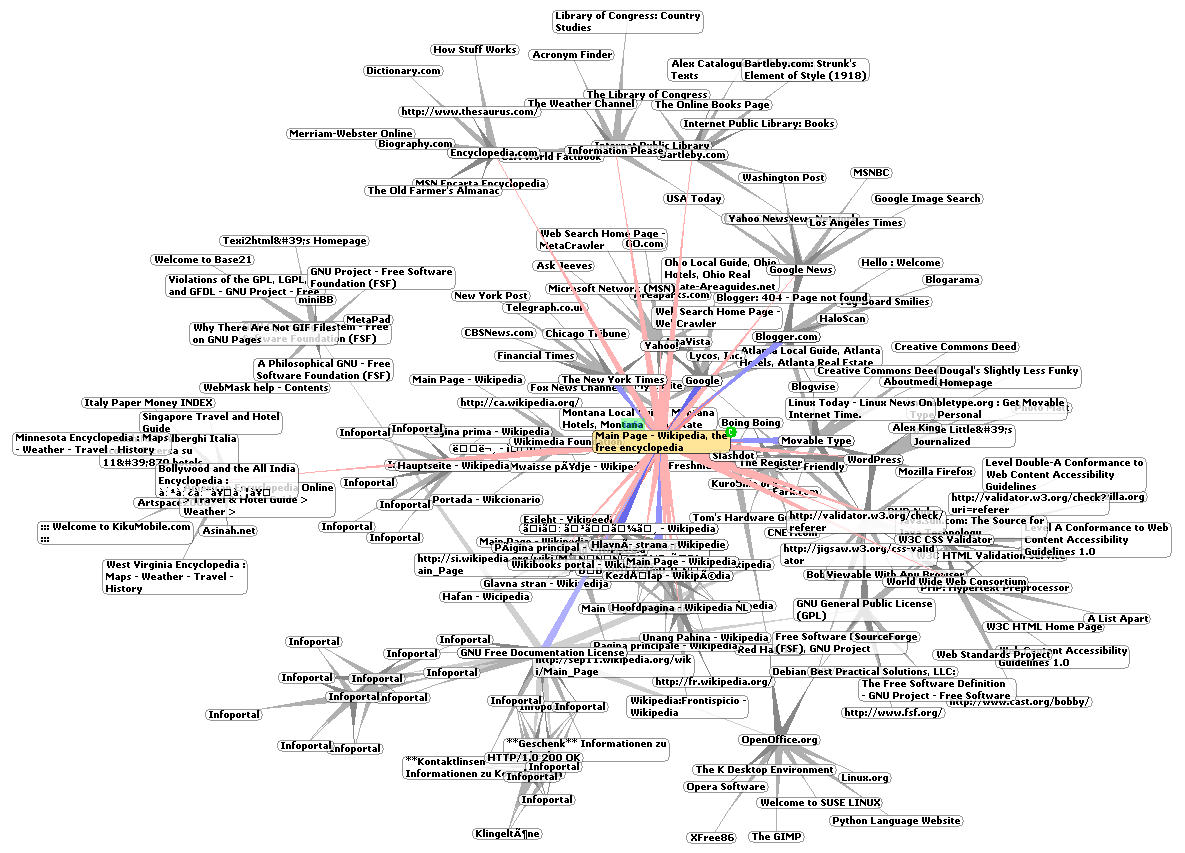
- WWWでは、ごく少数のメジャーなサイトが数百万単位のリンクを集めているが、大多数のサイトはわずかなリンク先関係しか持たない。
ベキ乗則に従うネットワークは、グラフのどの部分を取り出して拡大しても同じ形(相似形)となることから、スケールフリーネットワークとも呼ばれます。
画像出典:Wikimedia Commons Author : Chris 73
参考
べき分布における平均と分散について
統計処理において、平均と分散は非常に意味のある母数ですが、ベキ分布においてはこれが意味を持たない場合があります。
| 分布 | 平均 | 分散 | 特徴 |
| 正規分布 | 文字通り代表値 | 平均値からの散らばり具合 | ランダム |
| ベキ分布 | 意味がない場合がある | 意味がない場合がある | ロングテール |
Longtail とFattail
- Longtail
IT用語です。メインストリームでないニッチな勢力が集まることにより、大きな勢力となり得ることを示した概念用語で、メインストリームを「恐竜の首」とすると、ロングテールは「恐竜の長い尻尾」。Web2.0の時代において頻繁に登場するようになった言葉です。
- Fattail
金融用語です。通常起こらないような危機的な状況が意外に頻繁に起こり得ることを示した概念用語で、日本のバブル崩壊や、サブプライム危機は Fattail とされます。
関連ページ
- ツリー構造とセミラティス構造 Christopher Alexander
- 伽藍とバザール Eric Steven Raymond
- スケールフリーネットワーク Albert-László Barabási / Réka Alber
- 中心と周縁