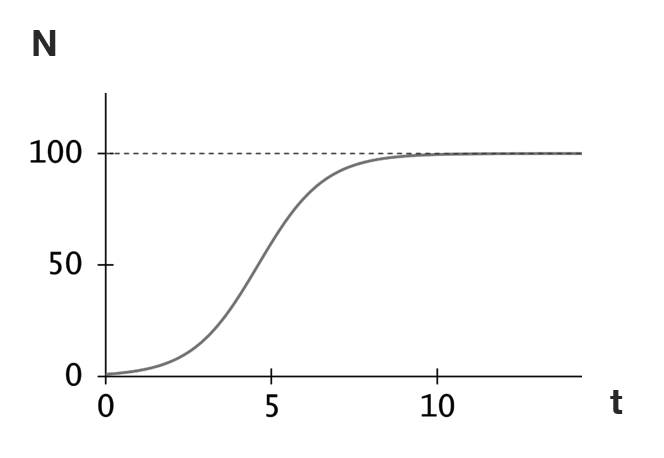
ロジスティック曲線
成長というものについて
概要
いわゆる「成長曲線」のひとつとして知られるロジスティック曲線は、ロジスティック方程式から導かれます。
ロジスティック方程式
生物の個体数の変化の様子を表す数理モデルの一種です。ベルギーの数学者ピエール=フランソワ・フェルフルスト(Pierre-François Verhulst)が1838年に発案したもので、単一種の生物が一定の環境内で増殖する場合に、その生物の個体数(個体群サイズ)の変動を予測する微分方程式です。
- N :個体数、
- t :時間、
- dN/dt :個体数の増加率を意味する。
- r :内的自然増加率、
- K :環境収容力
この式は、個体数が増えて環境収容力に近づくほど、個体数増加率が減っていくことを意味します。
ある生物の定着が成功するには大きな r を持つことが重要で、絶滅の回避には大きな K を持つことが重要だと言われます。ちなみにそれぞれが原因で淘汰されることを r淘汰、K淘汰と言います。
ロジスティック曲線
ロジスティック方程式の解(個体数と時間の関係)は、以下の関数式となり、右図のようなS字型の曲線を描きます。グラフは、r=1, K=100, N0=1の場合です(N0は初期個体数)。
人間にとってのロジスティック曲線
ロジスティック曲線を、人間社会における人口の推移を説明するモデルとして考えると、今何が起きているのか、その現状が見えやすくなります。
- 1970年代の爆発的な成長はカーブの中央、最も勾配の大きな部分に該当
- その後、人口の「増え方」は減速
- 現在は、水平に安定する「未来」への過渡期
しかし、従来の成長路線をそのまま踏襲すれば破滅の可能性がある人間にとってロジスティック曲線が現実に成立するのは、 20世紀末のグローバリゼーションにおいて、 地球という惑星の全体が現実に一つの有限性「閉域」として 立ち現れた以後である。
見田宗介「現代社会はどこに向かうか」岩波新書
人類が他の生物と異なるのは、テクノロジーによる「環境収容力の拡大」です。テクノロジーがなければ、人類の数は大型類人猿と同等数を上限にカーブ右上の安定期に入っていたでしょう。
- 出アフリカ > 生息域の拡大(地球全体へ)
- 農業革命 > 食料供給量の拡大
- 工業革命(産業革命)> 生活環境の拡大
- 情報革命 > 知の共有による対応力の向上
- 宇宙開発?> 生息域を宇宙へと拡大?・・多分現実的ではないと・・・
1970年代、人類は、テクノロジーの発展の先に「明るい未来」を想像し、「目標」を設定し、そこに向かって成長することに価値を見出していました。しかし、物質的な飽和状態を迎えた21世紀、人類には「向かうべき未来」が見えにくくなっているようです。商業的なデザインによって無尽蔵に作り出される「欲望」にも、そろそろ飽きたのではないでしょうか。
現在、一個体あたりの「資源消費量」は他の動物と比較にならないほど大きく、それが環境に大きなダメージを与え続けています。地球が有限の「閉域」であることが露呈した今、環境リスクの大きな「テクノロジーによる環境容量の増大」を期待するよりも、「脱・成長」を前提に「成熟期」の価値観で「幸福とは何か」を考えるべきかもしれません。
21世紀の若い世代は、成長期の代名詞ともいえる自動車には興味がなく、小さくてシンプルなもの、未来よりも今・・という生き方を好むようです。ヒトもやはり地球上の生物の一種、自然に正しい道を選択しようとしているのではないでしょうか。
APPENDIX
成績の伸び方
- はじめのうちはがんばってもあまり成績は上がらない
- あるタイミングから伸び始め、7割あたりまではグングン伸びる
- しかし、90点あたりから先はなかなか伸びず、100点を取るには相当な学習時間が必要になる
で、受験対策では、80点取れる科目をさらに伸ばすより、今30点台の苦手科目を伸ばすことを考える方が、短時間で総合点を上げることができる・・という発想になるわけです。
数値目標ってどうなんでしょう
世の中なんでもかんでも「数値目標を掲げろ!」と言われますが、毎年これを続けていると、最終的には100%を目指すことになってしまいます。これは巨視的に見ると弊害が多いので注意が必要です。
- 人事評価
個人が自己評価を上げるために猛進すると、自分の評価とは関係のない仕事には目を向けなくなります。特に80点から100点へ・・となるとなおさら自分のことだけに専念するようになる。あなたは80点で十分です。あとは伸び悩んでいる人を応援して下さい。
という組織の方が、全体のパフォーマンスが上がります。個別評価による競争が全体のパフォーマンスを下げるというのは既知の事実です。
- 組織評価
組織単位(モジュール)ごとの評価でも同じです。組織のクラッシュというのは、モジュールとモジュールの間で起きることが多い。他のモジュールへの目配せができない孤立したモジュールの集合体では、いつか大きな破綻が生じます。「なんでここに誰も気づかなかったのか」という大事故が増えています。そしてみんながこう答えます「それはうちの管轄ではなかった」。組織モジュールごとの熾烈な競争が招いた結果です。
完璧主義の弊害
- 社会の問題解決
100人いれば悪い事をするのが2〜3人はいる。問題を0にしようとすると
・追加の法律が必要になる
・追加の人的資源が必要になる
問題の発生を未然に防ぐためのアンケート調査や報告業務が増える
責任回避のためのアリバイづくりの業務が増える
・恒常的な組織や「箱物」が必要になる
これら、すべて社会の負担になります。結果、被害額よりも大きな予算が必要になるだけでなく、問題のない人にまで余計な縛りが発生して世の中どんどん息苦しくなります。想定される被害の大きさと、それを防ぐのに必要なコストとのバランスを考える必要があります。
- 収穫
100%の収穫を目指して肥料や農薬を撒く、鳥や虫を排除する・・そんなことをすると、土壌の生産力が失われます。
- 除菌
100%除菌したら生態系は破綻します。分解者としての菌の存在に感謝する気持ちも必要です。撲滅ではなく上手に棲み分けるというのが正解でしょう。
デジタル化・オンライン化による可能性
- 紙媒体の出版では、誤字・脱字を限りなく0にすべく「校正」というプロセスに多くの時間と労力が必要でした。一方、Webの記事の場合、極端な例では、書けるところだけ書いて、「書きかけです」として公開してしまうこともできます。
- 未完のままリリースして、アップデートによって安定・成熟することを前提とするデジタルの世界では、ソフトの βバージョン公開と同様「校正作業」の多くを発信側ではなく受信側に委ねることが可能で、その方が圧倒的に短時間で修正・アップデートが可能になります。これは、成長曲線の右端部分の効率化に寄与しているといえるでしょう。
常に生産完成品として発行されて、やがてゴミになる「モノ」に対して、更新しつづける動的な「情報」に可能性を感じます。