InformationTheory

情報理論

InformationTheory

↑

はじめに

情報とは、何らかの媒体を通じて発信者から、受信者に伝達される意味内容のことです。人間同士の会話、紙に記された文字、モニターに表示される映像、音楽、さらには、ネットワークを行き交う信号など、様々な様態があります。

↑

informationの語義・語源

information n.
1. informすること
2. 告訴、略式起訴
inform v.
1. 教育する、訓練する
2. 形づくる、生み出す
3. 知識を授ける、教える
4. …の特徴を与える；魂を吹き込む
5. 人に…を知らせる
informer n.
1. 教授者、指導者
2. 通知者、情報提供者

英語語源辞典,1997,研究社

↑

物質・エネルギー・情報

物質・エネルギー・情報という３大抽象概念のうち、「情報」は科学の対象としては歴史的に最も新しい概念です。

物質（紀元前） ＞ エネルギー（17世紀） ＞ 情報（19世紀）

物質は、我々の視覚・触覚で直感的に捉えられるもので、デモクリトスの原子論以来、紀元前から思考の対象となっていました。

デモクリトス（BC.460頃～ BC.370頃）　原子論
アリストテレス（BC.384 ～ BC.322）　質料と形相　形相は「情報」概念の萌芽

エネルギーは、直接的に目に見える対象ではないがゆえに、その理解には時間を要しました。

力学的エネルギー（運動エネルギー＋位置エネルギー）
熱エネルギー
化学エネルギー（結合、燃焼）
電磁気エネルギー（電気、磁気）
電磁波エネルギー（光、放射線）
核エネルギー（核分裂、核融合）

17世紀イタリアの物理学者ガリレオ・ガリレイによる「位置エネルギーと運動エネルギー（力学的エネルギー）の保存」の発見がエネルギー概念の萌芽で、それから 200年以上を経た 19世紀、イギリスの物理学者ジュール（他にマイヤーとヘルムホルツ）が、エネルギー保存則（熱力学の第１法則）を確立しました。

力学的エネルギーに加え、熱エネルギー、化学的エネルギー、
電気エネルギー、光（電磁波）のエネルギー・・
すべてのエネルギーの総和は、閉じた系において常に一定である。

これによって、あらゆる物理現象が数式によって説明されるようになり、同時に、人類は対象を思い通りに制御する術を手に入れました。

そして1905年、物理学者 A. アインシュタインの特殊相対性理論により、

 物質とエネルギーは同じものであり、相互に変換できる

ということが発見されました。質量とエネルギーは E = mc2 という関係にあり「閉じた系において質量とエネルギーの総和は常に一定」であることがわかったのです。ちなみに c（光速）は 299,792,458 m/s という非常に大きな数なので、この式は、わずかな質量が膨大なエネルギーに置き換わることを意味します。

では、情報とは何か。それは、サイバネティックス（人工頭脳学）の生みの親である、数学者 N.ウイナーによって、以下のように説明されます。

物質・エネルギーが存在する様態、すなわち、
時間的・空間的、定性的・定量的なパターンが「情報」である

情報とは何か。物質・エネルギー・情報という３つの概念を並べて、その発見の歴史を眺めてみることで、情報媒体（物質・エネルギー）と情報（時間的・空間的パターン）という、総合的な理解のための２つのキーワードを手に入れることができます。

物質として存在する情報媒体は空間に拘束されるとともに、時間の流れに逆らうことができませんが、情報は、空間・時間を超越します。

↑

パターンとコード

パターンとコード。似ているようで異なる概念です。パターンは物理的な要因のみでも発生しますが（散逸構造）、コードの生成には「意志」が必要です。

Pattern：規則性のある様式、模様、型、体系・・・
Code：法、規則、規約、慣例、作法、記号、符号、識別子・・・

↑

情報を捉える視点（概念モデル）

情報は主に「視覚情報」「聴覚情報」（「触覚情報」）に分類できる
これらは光・電波・音波・力といった物理的な存在であり、電気・電子的な情報として様々な媒体によって転送・蓄積することができます。「味覚情報」「嗅覚情報」も情報ではありますが、これらは化学的なもので、その発生・転送・蓄積・再生に関する技術は発展途上にあります。

情報は、「情報源」から発生し「情報媒体」に載って移動する
- 聴覚情報：情報は「音源」から発せられる
- 視覚情報：情報は「二次光源」上にある（「光源」がそれを照らす）

情報にはアナログ（類似・連続的）とデジタル（数値・離散的）がある
- アナログは情報と媒体が一体となっている（フィルム、アナログレコード）
- デジタルは情報と媒体が独立している（USB、ネットワークドライブ・・）

情報はハードとソフトの区別でいえばソフトにあたる
- ハード（モノ）は劣化してやがてゴミになる
- ソフト（情報）はバージョンアップするとともに半永久的に利用が可能

情報は「有限の要素」の配列として編集される
文字は有限の要素の集合で、個々の文字にはコードが割り当てられている
参考：文字コードの確認

情報は複製される
- 情報は物質ではないため複製コストがかからない（限界費用０）
- 複製・共有されない情報は情報として機能しない

情報は「生産完成品」ではない（送り手側だけで成立するものではない）
- 工場で生産される「製品」の大半は「生産完成品」
- 文学・映像・音楽・・いずれも「受け手」の状態が関与する

↑

情報理論に関わる重要な人物

ノーバート・ウィーナー（1894 - 1964）：サイバネティクス
フォン・ノイマン（1903 - 1957）：計算機科学・ストアドプログラム
クロード・シャノン（1916 - 2001）：情報理論・情報量（エントロピー）

↑

情報量と秩序

情報量の定義には、「その事象がもたらす知らせの大きさ」として定義するものと、「可能性のある事象の全体から想定される知らせの大きさの期待値（平均値）」として定義するものとがあります。前者を選択的情報量、後者を平均情報量（エントロピー）と呼んで区別します。

↑

選択的情報量

事象Eが起こる確率を P(E) とするとき、「事象 E が起こったという知らせ」がもたらす情報量 I(E) を以下のように定義します。

\[ I(E) = \log_{2}{ \frac{1}{P(E)} } = -\log_{2}{P(E)} \]

情報量は、2を底とする対数で、単位は bit（ binary digit ：２進数）です。
生起確率が低い事象ほど情報量は大きくなる。つまり「珍しい話ほど、情報量は大きい」という、ごくあたりまえの話として理解できます。

選択的情報量は、事象によっては簡単に記述することもできます。例えば６通りの可能性のあるサイコロで１の目が出る確率は 1/6 なので、「１が出た」という知らせがもたらす情報量はー log 2 (1/6) = log 2 6 = 2.5849 (bit) となります。このサイコロのように、個々の「生起確率」が等しい場合、その逆数である「可能性の数 \( N \)」を使うと計算式が簡単になります。

\[ I(E) = \log_{2}{N} \]

↑

対数について

\( \log \) って何？という方へ、以下のように理解いただくだけで十分です。

\( \log_{2}8 = 3 \) とは「２を３乗したら８になる」という関係を意味します。
つまり \( \log_{2}8 = \) は「２を何乗すれば８になるか？」という問いで、
「２を底とする８の対数は３である」などという言い方をします。
で、例題、 \( \log_{2}256 = 8 \) （2を底とする256の対数は８）です。
以下、参考までに \( y = \log_{2}X \) のグラフです。
Google: y = log2 x

ちなみに、 \( \log_{2}16^2 = 2 \times \log_{2}16 \)（どちらも 8）
つまり、指数はくくり出せるので、
\( - \log_{2}\frac{1}{N} = - \log_{2}N^{-1} = \log_{2}N \) ということになります。
事象の出現確率がすべて同じであれば、 \( p = \frac{1}{N} \) ということになるので、 \( -\log_{2}P \) と \( \log_{2}{N} \) は同じこととして説明できます。

↑

平均情報量（エントロピー,シャノン情報量）

すべての事象について「出現確率 x 出現時情報量」の平均をとった値、すなわち選択的情報量 \( -\log_{2}{P(E)} \) の「期待値」H(P) を平均情報量（エントロピー）といいます。

\[ H(P) = - \sum_{ }^{ } P(E) \cdot \log_{2}{P(E)} \]

↑

エントロピーは何を意味するか

情報学におけるエントロピーは、簡単にいうと「わからなさ」の指標です。
結果が「どの程度予測しにくいか」といってもいいでしょう。
この概念を用いると、以下のように情報量を考えることができます。

ある「知らせ」の情報量
　= はじめのわからなさー「知らせ」のあとに残るわからなさ

サイコロを振ったとき「偶数が出てるよ」という「天使のつぶやき」の情報量を計算してみましょう。

サイコロを振って何がでるか？の、はじめのエントロピーは、
ー Σ(1/6)・log 2 (1/6)　
= ー 1/6 x log 2 (1/6) ー 1/6 x log 2 (1/6) ・・・ー 1/6 x log 2 (1/6)
= ー log 2 (1/6) = log 2 6 = 2.5849 (bit)
「偶数が出てるよ」というつぶやき（ヒント）が得られたとすると、
あとは２か４か６なので、あとに残るエントロピーは
ー Σ(1/3)・log 2 (1/3)　
= ー 1/3 x log 2 (1/3) ー 1/3 x log 2 (1/3) ー 1/3 x log 2 (1/3)
= ー log 2 (1/3) = log 2 3 = 1.5849 (bit)
3) よって「偶数の目が出た」という知らせの情報量は、
　情報量 = 1) - 2) = log 2 6 - log 2 3 = log 2 2 = 1 (bit)
「偶数の目」がでる確率は 1/2 なので、
選択的情報量である - log 2 (1/2) = 1 (bit)　と一致する。

サイコロのように、すべての事象の出現確率が均等である場合、結果的には、平均情報量は、ふつうに選択的情報量を計算した場合と同じになります。

しかし、実際には事象ごとに、出現確率は異なります。
例えば、水[　] の空欄を埋める問題では、水[色]や水[曜]は比較的出現しやすいですが、水[鶏]（くいな）はめったに出現しません。水[曜]を答えさせるクイズは簡単で、水[鶏]を答えさせるクイズは難問となります。よって、単純に[　]に入る可能性のある文字が何通りあるかだけでは、エントロピーを計ることはできず、理論的には、 - ΣP(E)・log 2 P(E) と、すべての事象について合算平均する必要が生じるのです。

参考：熱力学におけるエントロピー

↑

なぜ対数を使うのか

刺激・情報に対する人間の感覚は、物理量の対数をとるとちょうどいい・・
というのが対数をとる理由です。

例えば、ひらがな２文字と４文字で、表現できる量を比較してみます
- ２文字(2桁)で表現できるのは、502 = 2,500通り
- ４文字(4桁)で表現できるのは、504 = 6,250,000通り　
  ということで、４文字は２文字の 2,500倍の表現が可能です。

しかし人間の感覚では、「４文字は２文字の２倍」という感じ。
「桁数」をそのまま情報量とする方が直感に合います。

そこで、表現できる数について、50を底とする対数をとると
- ２文字(2桁)の場合は、log 50 2,500 = 2
- ４文字(4桁)の場合は、log 50 6,250,000 = 4
  と「桁数」に戻って、人間がふつうに感じる「情報の量」に一致します。

ちなみに、bit(binary digit)という単位は、２を底とする対数に由来。
２進数の世界では、N桁で２Nとおりの表現が可能なので、
log 2 2 N = N bit　つまり桁数がそのままビット数になります。

↑

事例研究

コインを投げたとき・・「表が出た」という「知らせ」がもたらす情報量は
可能性の数で考えれば log 2 2 = 1 (bit)
出現確率で考えれば - log 2 (1/2) = log 2 2 = 1 (bit)

音域１オクターブのメロディーで1音が担う情報量は
- ７音階→８音　log 2 8 = 3 (bit)
- ５音階→６音　log 2 6 = 2.585 (bit)

1文字が担う情報量は
- 英語（アルファベット）：log 2 26 = 4.7
- 日本語（ひらがな）：log 2 50 = 5.644
  英語を日本語に訳すと文字数が少なくなるのは、日本語１文字が担う情報量の方が大きいから・・と説明できます。

２進数８桁が担う情報量は、
0000 0000 〜 1111 1111 → 2x2x2x2x2x2x2x2 = 256 通り
log2256 (bit)　= 8 (bit)　
一般に、２進数N桁の情報量は N (bit) になります。

キーボード上にある英字、数字、記号、１タイプが担う情報量は
英字、数字、記号の総数は約200種類　log 2 200 = 7.64 (bit)
つまり　8ビット＝1バイト　というのは、
欧米の人が使う文字を１つ表現するのに必要な情報量・・・に由来します。

↑

参考：関数電卓で対数計算

関数電卓で \( \log_{2}256 \) を計算したい場合は、以下のように入力します。

log(256,2)

↑

情報量と感じ方

情報量が小さすぎる：単調退屈おもしろくない
情報量が適度に大きい：なるほど! 面白い!
情報量が大きすぎる：複雑難解不快感

↑

「秩序」について

情報とは、外界から得る知識内容のことであり、
記号のセリーが担っている秩序の尺度である(N.ウイナー)。

人間は自ら秩序を作る生き物であり、また記号的に世界を
秩序立てて見ようとする生き物だといえます。

人間の作る秩序には、先行するイメージとしての設計図、
すなわちデザインがあります。

「最も巧みな蜜蜂と最も無能な建築家の違いは、
建築家が設計図にもとづいて仕事をすることである。」
　　　　　　P.J.Wilson(『人間-約束するサル』佐藤俊訳)

↑

秩序(情報)を捉える「知識ベース」について

あらゆる情報の認知には、「基準」や「準拠枠（Frame of Reference）」が必要です。それらは見る者の「構え」を形成し、情報要素はトップダウン的にその基準からの偏移によって測られます(音楽では曲のキーやスケールが「基準」に該当)。

例えば、桜が美しくみえるかどうか・・・という話しでも、
それを見る者の「桜についての知識のありかた」が大きく影響しています。

↑

情報の哲学

↑

情報の空間性・時間性

松岡正剛(「知の編集工学」)に、有名な言葉があります。

情報は、ひとりでいられない

我々が「情報」をどのように扱っているか、また遺伝「情報」はどのようにふるまっているかをみれば明らかですが、情報は複製・伝達・蓄積・共有されることで、はじめて意味をもつ存在です。　・・情報の時間性
例えば、「赤」は単体では意味をもちませんが、「青」と組み合わされて「交差点」という文脈に位置付けられると「止まれ」という意味を担う情報になります。他との「関係」が重要なのです。・・情報の空間性

↑

差異/言語/情報

最も基本的な「情報化」は、それに「名を与える」ということです。
言語化されてはじめてそれは情報になります。 > 言葉とは何か
物事を「差異化」して「関係づけ」すること・・

↑

情報デザインの起源

ブレンダ・ダービン(「情報デザイン原論」)によれば、「情報」は、それ自体、人間がデザインした(ている)もの・・と考えることができます。

「情報」は、無秩序でもあり、秩序でもある現実を明快に理解するために
人間が考案（デザイン）した道具である。　ブレンダ・ダービン

情報の起源 > イメージの起源
人はなぜ「情報」を遺すのか？（時間軸比較）
- ホモサピエンス
- 人類拡散のルート
類人猿は「情報」を扱うのか？（水平軸比較）

↑

情報量と視覚情報デザイン

↑

平面構成と情報量

↑

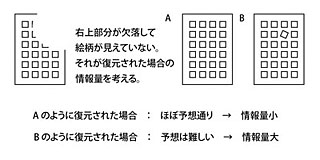
文脈(コンテキスト)によって変化する情報量

文脈からある程度推理できる情報要素の出現 → 情報量小
文脈からは推理しにくい情報要素の出現 → 情報量大

筆箱とペンと三角定規　←→　土曜日とペンと腕時計　
筆箱・三角定規に並置された「ペン」と、土曜日・腕時計に並置された「ペン」とでは、後者の方が出現確率が小さく情報量が大きなものになります。後者の「ペン」は、筆記具としての意味以上のイメージの広がりを持ちます。

空を見上げて　←→　空を持ち上げて
文脈的に推測しにくい言葉が出現するという点で、上と同様に
右の表現の方が情報量の大きな表現といえます。

↑

編集によって変化する情報量

要素が単体で存在する状態 → 情報として認知されにくい
要素を反復(リフレイン)すると → 秩序感が生まれる（人間の意志を感じる）
秩序のルールが単純・強固になると → 情報量は減少する
秩序に偏移を与える(対称性を破る)と → 緊張感増大/情報量増大

偏移が激しくなると → 情報量は増大するが、それがあまりにも過度になれば、単に無秩序な状態に見え、情報として認知されにくくなります

同じ情報要素(映像で言うショット)も、編集によって前後関係を入れ替えるだけでも情報量が変化します。

↑

身近な「情報」の情報量を上げるには？

言葉の順序を変える　「地球の [ 水 ] 」　→　「水の [ 地球 ] 」
物事を「斜め」につなぐ、異なる地平にあるものをつなぐ
- 例）「ひらがな」を「洗う」
  ひらがな｜で…｜に…｜を…｜は …｜が…｜も…｜へ…｜

↑