「高校1年生を対象とした物理基礎の理解をサポートするデザイン研究」の版間の差分
(→参考文献・参考サイト) |
細 (「高校1年生を対象とした物理基礎の理解をサポートするデザイン研究」を保護しました ([編集=管理者のみ許可] (無期限) [移動=管理者のみ許可] (無期限))) |
||
| (2人の利用者による、間の10版が非表示) | |||
| 1行目: | 1行目: | ||
| − | |||
| − | + | ; 大渕浩史 / 九州大学大学院芸術工学府 | |
| − | + | : OBUCHI Hirofumi / Kyushu University | |
| − | + | ; 平井康之 / 九州大学大学院芸術工学研究院 | |
| − | + | : HIRAI Yasuyuki / Kyushu University | |
| − | |||
| − | |||
| − | |||
| − | + | ''Keywords: Social Design, Learning Design'' | |
| − | |||
| − | |||
| − | |||
; Abstract | ; Abstract | ||
| − | : | + | : For first-year high school students who enter high school and begin to learn physics basics, we extract issues related to understanding learning content from the perspective of communication design, and extract requirements to support future understanding of physical physics. |
| + | ==目的と背景== | ||
| + | 文部科学省は、平成29年9月の高等学校の学習指導要領の改訂で: | ||
| − | + | 知識を相互に関連付けてより深く理解したり、情報を精査して考えを形成したり、問題を見いだして解決策を考えたり、思いや考えを基に創造したりすることに向かう過程を重視した学習 | |
| − | + | ||
| − | + | の必要性を述べている(高校学習指導要領)。また来年度から始まる大学入学者選抜改革により、従来マーク式であったセンター試験を記述式の大学入学共通テストに変更にすることで、パターン暗記型の学習ではなく、より深く知識を理解して、問題で応用していく力が求められている。 | |
| − | + | ||
| − | + | そこで本研究は、高校に入学して物理基礎を学び始める高校1年生を対象に、コミュニケーションデザインの視点から学習内容の理解に関する課題を抽出し、今後の物理基礎・物理の理解をサポートするための要件を抽出することを目的とする。 | |
==研究の方法== | ==研究の方法== | ||
| 39行目: | 34行目: | ||
フィールド調査の目的は、第一に高校1年生が物理を学習、理解する上での課題を抽出することである。次にデザイン提案の検証、評価を行うことである。 | フィールド調査の目的は、第一に高校1年生が物理を学習、理解する上での課題を抽出することである。次にデザイン提案の検証、評価を行うことである。 | ||
===答案調査=== | ===答案調査=== | ||
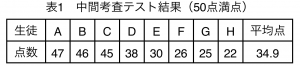
| − | 1つ目の調査は2019年5月に学習塾の全教研柳川校の高校1年生を対象にフィールド調査を行なった。調査の内容としては、高校で行われた中間考査の物理の答案を8人の生徒から見せてもらい、問題に対するアプローチの仕方、課題の分析を行った。8人の平均点は50点満点中34. | + | 1つ目の調査は2019年5月に学習塾の全教研柳川校の高校1年生を対象にフィールド調査を行なった。調査の内容としては、高校で行われた中間考査の物理の答案を8人の生徒から見せてもらい、問題に対するアプローチの仕方、課題の分析を行った。8人の平均点は50点満点中34.9点であった(表1)。正答率が低かった問題としては、高校1年生がまだ学習していない数学ⅡBの範囲であるベクトルや微分の単元の知識を必要とする問題であった。また、ベクトル量を扱う問題の正答率も低く、これはベクトル量自体の扱いができておらず答え方の段階で間違えている生徒が多かった。 |
[[ファイル:表1.png|サムネイル|答案調査結果]] | [[ファイル:表1.png|サムネイル|答案調査結果]] | ||
===基礎知識確認調査=== | ===基礎知識確認調査=== | ||
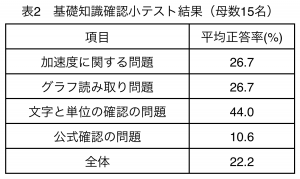
| − | 2019年6月に2回目の調査を行い、基本的知識がどれだけ分かっているかの確認のために高校1年生15名に小テストを行った。出題範囲は等加速度直線運動の単元で行なった。問題内容としては、物理基礎の問題集の知識や公式のまとめ問題で使われている内容で、その単元に必要とされる公式、a(加速度)、v(速度)、t(時刻)などの公式で使われる文字が何を表しているのか、さらに、その文字の単位は何か、グラフの読み取りや等加速度直線運動の公式など問題を解くのに必要な基礎知識の内容で行った。結果として15名の平均正答率は22. | + | 2019年6月に2回目の調査を行い、基本的知識がどれだけ分かっているかの確認のために高校1年生15名に小テストを行った。出題範囲は等加速度直線運動の単元で行なった。問題内容としては、物理基礎の問題集の知識や公式のまとめ問題で使われている内容で、その単元に必要とされる公式、a(加速度)、v(速度)、t(時刻)などの公式で使われる文字が何を表しているのか、さらに、その文字の単位は何か、グラフの読み取りや等加速度直線運動の公式など問題を解くのに必要な基礎知識の内容で行った。結果として15名の平均正答率は22.2%と低かった。項目別で見ると、文字と単位の確認が、1番正答率が高かったがそれでも44.0%と低い数値であった。公式の問題に関しては正答率が10.6%とほとんどの生徒が公式を覚えていないという結果が得られた。このことから生徒の大半が問題を解く段階まで理解が達していないことがわかった(表2)。 |
[[ファイル:表2.png|サムネイル]] | [[ファイル:表2.png|サムネイル]] | ||
| 91行目: | 86行目: | ||
*山崎真弘(2019)『高校物理の読解プロセスと情報の図式化のデザイン研究』 | *山崎真弘(2019)『高校物理の読解プロセスと情報の図式化のデザイン研究』 | ||
*今村吉孝(2019)『高校物理の教科書にて用いられる数式と高校数学のカリキュラムの関連について』 | *今村吉孝(2019)『高校物理の教科書にて用いられる数式と高校数学のカリキュラムの関連について』 | ||
| − | *今泉洋(2015)『実はカンタンな図解の技術』 | + | *今泉洋(2015)『実はカンタンな図解の技術』 http://scholar.tokyo/vol12/ |
| − | http://scholar.tokyo/vol12/ | ||
*吉岡有文(1988)『物理の理解とメンタルモデル』 | *吉岡有文(1988)『物理の理解とメンタルモデル』 | ||
<br> | <br> | ||
2020年8月5日 (水) 16:31時点における最新版
- 大渕浩史 / 九州大学大学院芸術工学府
- OBUCHI Hirofumi / Kyushu University
- 平井康之 / 九州大学大学院芸術工学研究院
- HIRAI Yasuyuki / Kyushu University
Keywords: Social Design, Learning Design
- Abstract
- For first-year high school students who enter high school and begin to learn physics basics, we extract issues related to understanding learning content from the perspective of communication design, and extract requirements to support future understanding of physical physics.
目的と背景
文部科学省は、平成29年9月の高等学校の学習指導要領の改訂で:
知識を相互に関連付けてより深く理解したり、情報を精査して考えを形成したり、問題を見いだして解決策を考えたり、思いや考えを基に創造したりすることに向かう過程を重視した学習
の必要性を述べている(高校学習指導要領)。また来年度から始まる大学入学者選抜改革により、従来マーク式であったセンター試験を記述式の大学入学共通テストに変更にすることで、パターン暗記型の学習ではなく、より深く知識を理解して、問題で応用していく力が求められている。
そこで本研究は、高校に入学して物理基礎を学び始める高校1年生を対象に、コミュニケーションデザインの視点から学習内容の理解に関する課題を抽出し、今後の物理基礎・物理の理解をサポートするための要件を抽出することを目的とする。
研究の方法
文献調査では「理解力」、「読解力」についての内容と「物理の学習」についての既往研究調査と先行事例調査を行い、「物理の理解」について必要、または効果的な要因を抽出する。 フィールド調査では、大きく分類して2つ行う。1つ目は、高校1年生が物理を学習、理解する上での課題を抽出することである。2つ目は、デザイン提案の検証、評価を行う。 さらに、文献調査とフィールド調査をもとに、考察を行い物理の理解における課題を抽出する。その課題をもとに、ツールを作成し、その有用性を検証し、評価してもらう。
文献調査
今村(2019)は『高校物理の教科書にて用いられる数式と高校数学のカリキュラムの関連について』の中で、物理基礎の力学の範囲で用いられる式の数が70あるのに対して中学以前の数学の知識を必要とする式の数が24、微分・積分の知識を必要とする式の数が12、ベクトルの知識を必要とする式が34あると述べている。ベクトルに関しては、物理基礎の力学範囲の式の数の48.6%を占めている。また微分・積分の式に関しては、微分・積分の単元と明記せずに記載されているのに対して、ベクトルが関わる式はベクトルの考え方を使わざるを得ないので、ベクトルの理解が必要となる。
フィールド調査
フィールド調査の目的は、第一に高校1年生が物理を学習、理解する上での課題を抽出することである。次にデザイン提案の検証、評価を行うことである。
答案調査
1つ目の調査は2019年5月に学習塾の全教研柳川校の高校1年生を対象にフィールド調査を行なった。調査の内容としては、高校で行われた中間考査の物理の答案を8人の生徒から見せてもらい、問題に対するアプローチの仕方、課題の分析を行った。8人の平均点は50点満点中34.9点であった(表1)。正答率が低かった問題としては、高校1年生がまだ学習していない数学ⅡBの範囲であるベクトルや微分の単元の知識を必要とする問題であった。また、ベクトル量を扱う問題の正答率も低く、これはベクトル量自体の扱いができておらず答え方の段階で間違えている生徒が多かった。
基礎知識確認調査
2019年6月に2回目の調査を行い、基本的知識がどれだけ分かっているかの確認のために高校1年生15名に小テストを行った。出題範囲は等加速度直線運動の単元で行なった。問題内容としては、物理基礎の問題集の知識や公式のまとめ問題で使われている内容で、その単元に必要とされる公式、a(加速度)、v(速度)、t(時刻)などの公式で使われる文字が何を表しているのか、さらに、その文字の単位は何か、グラフの読み取りや等加速度直線運動の公式など問題を解くのに必要な基礎知識の内容で行った。結果として15名の平均正答率は22.2%と低かった。項目別で見ると、文字と単位の確認が、1番正答率が高かったがそれでも44.0%と低い数値であった。公式の問題に関しては正答率が10.6%とほとんどの生徒が公式を覚えていないという結果が得られた。このことから生徒の大半が問題を解く段階まで理解が達していないことがわかった(表2)。
答案作成調査
基礎知識確認の調査の後日、5名の生徒に答案作成の調査に協力してもらった。小テストを行った範囲で高校で使用されている問題集の基本問題レベルの内容の問題を解いてもらった。その結果、解けなった理由として、
(1)公式を正確に覚えていない
(2)公式は覚えているがどの公式を使うかわからない
(3)ベクトル量の扱いができておらず、作図・計算の時に矢印の向き・正負を逆にしてしまう
(4)単純な計算ミス
の4つが挙げられた。その中でも公式を覚えていない理由が正答率に大きく影響していた。また、5月に行なった答案調査と同様にベクトル量の扱いも、問題を特にあたっての課題となった。
結果
3つの調査結果から高校1年生の物理基礎の学習においての課題は
(1)ベクトルについての理解、扱い方
(2)基本的知識や公式の理解
(3)問題の読解力、解き方
の3つが挙げられる。
考察
結論で挙げた3つの課題のうち(3)の問題の読解力、解き方については山崎が作図において新しい記号を用いたアプローチを行っていた。さらに今回は問題を解くよりも前の段階である物理の理解に焦点をあてているので(1)と(2)の課題を解決する必要がある。ベクトルについての理解に関しては基本的知識や公式を理解していく段階で必要となる知識であるので、本研究では基本的知識や公式の理解を最重要課題とし、それらを理解していく段階でベクトルの知識も理解していく必要があると考える。
結論
物理基礎の力学の単元は私たちの日常生活での物理現象に密接に関わっている。吉岡(1988)は、物理の理解において一つ一つの現象の理解に正確なメンタルモデルを持つことが重要であるとしている。
また力学の各公式はそれぞれに関連性があり単独で存在する公式は少ない。そのような関係性の理解も必要になると考えられる。今泉(2015)は、情報を図式化することによって関係性を視覚的にスムーズに理解することができると述べている。
これらのことから、基本的知識や公式の理解を最重要課題とする上で、
(1)日常生活での物理現象と物理基礎(力学)のリンク
(2)公式や法則同士の関連性の図式化
を行っていくことが基本的知識や公式の理解のデザイン要件になると考える。
参考文献・参考サイト
- 文部科学省(2018)『高校学習指導要領』p4 本文10〜15行目
- 山崎真弘(2019)『高校物理の読解プロセスと情報の図式化のデザイン研究』
- 今村吉孝(2019)『高校物理の教科書にて用いられる数式と高校数学のカリキュラムの関連について』
- 今泉洋(2015)『実はカンタンな図解の技術』 http://scholar.tokyo/vol12/
- 吉岡有文(1988)『物理の理解とメンタルモデル』