正方形 3x3
-芸術工学的「正方形」研究III-
SQUARES 3x3 - Study on "SQUARES" in field of design
1.はじめに
一般的なデザイン研究では「はじめに解決すべき問題があって、そのために最適な形状を探る」というのが普通である。しかし、「ある特定の形状がどのような場面で活用されているかを探る」という、逆遠近法的かつ領域横断的な研究もまた可能である。
本研究は、ブルーノ・ムナーリが1960年に著した「IL QUADRATO(正方形)」註1)に触発されて着手した「正方形の活用事例研究」のひとつに位置づけられる。先行研究では「2×2」をキーワードとして「田の字型の造形」や「4つの正方形による造形」の事例を報告したが註2)、今回はそれに引き続き、「3×3」の事例について報告する。
2.調査の方法
調査は先行研究と同様、今和次郎註3)に倣って、「調査の現場において有効な統計項目を見出す」ことからはじめた。手順は以下のとおりである。
1)初期キーワードを「3×3」として、Web上で画像検索を行い、「正方形3×3」に結び付く様々なイメージを見出す。
2)次にそれらの画像から掲載元のページを辿り、記事本文の中からターゲットの出現に寄与するであろう2次的なキーワードを探る。
3)それらのキーワードによって再度検索を行い、条件に合うものを抽出して、空間、モノ、情報とデザインの領域別に分類整理する。
検索にはGoogle画像検索註4)を利用。いずれも大量にヒットするため、先行研究同様に、検索で上位にランクされる200件の画像を対象とした。
検索日は2012年8月1日~7日の間。検索に関わる詳細な条件は先行研究と同一である。
3. 調査に有効なキーワード
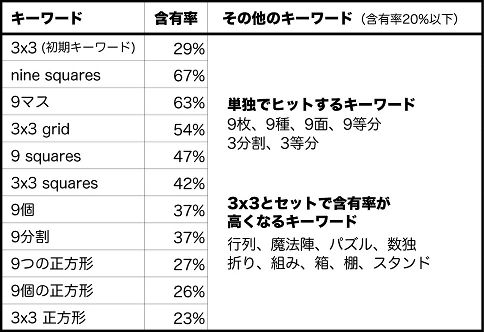
表1は調査の第一段階で得られた「正方形3×3」の出現に寄与するキーワードである。検索結果の20%(40件)以上で目的のイメージが得られるものを掲載している。
「3×3」という初期キーワードでは、出現した画像の29%ほどが「正方形3×3」のイメージに合致しており、先行研究における「2×2」の21%を上回った。
注目すべきは「9」という数字である。単に「9」だけでは効果がないが、「nine squares」や「9マス」では6割以上が「正方形3×3」のイメージを有しており、さらに9個、9分割、9枚、9種などでも、ターゲットを多数見出すことができた。「2×2」の場合の「four squares」や「4マス」と同様、「9」という数字は、「3×3」と強い相関をもつと考えられる。
その他、「折り」、「組み」、「箱」といった単語も注目に値する。これらの単語は「2×2」の場合にも同様の効果があったが、「3×3」という数字と組み合わせると、ターゲットの出現頻度が大幅に高くなることがわかった。
4.「正方形3×3」の活用事例
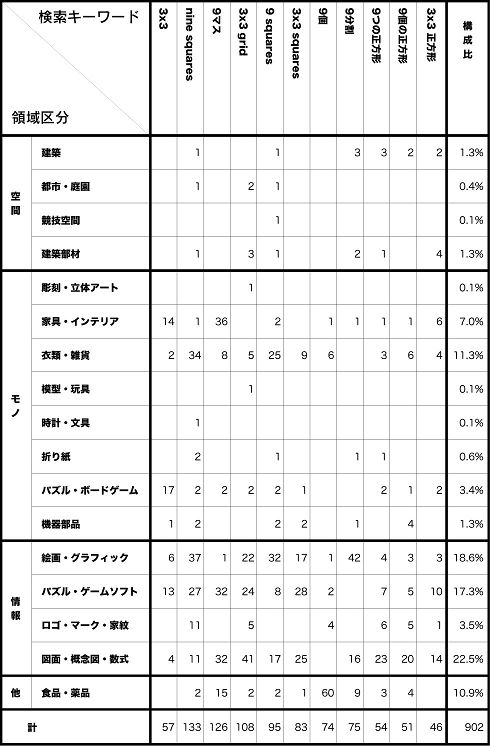
表2はデザインの領域別にターゲットの出現数を調べた結果である。「空間」のデザインでは、都市区画や建築物、「モノ」のデザインでは、家具、雑貨、玩具、機器部品、そして「(視覚)情報」のデザインでは、絵画・グラフィックから概念図まで、あらゆる場面に「正方形3×3」が存在していることがわかる。
構成比をみると、「空間」の事例が3%、「モノ」が24%、「情報」が62%、その他11%と、「情報」の領域の占める割合が圧倒的に多い。先行研究である「正方形2×2」の場合と比較したところ、建築、模型・玩具の項目が減り、逆に概念図等の占める割合が多くなっていることもわかった。
尚、今回の調査でも先行研究と同様、不完全な正方形(縦横比が1:1以外のもの)についても、有意義な資料と考えて、それらを含めている。
4.1. 空間のデザイン
検索の結果、数の上では空間のデザインに関わる活用事例は少なかったが、見出された画像には示唆に富むものも多かった(図1)。
まずスケールの大きなものとして、都市の区画がある。中国の都、またそれを模した日本の都など、計画された都市に正方形のグリッドが見られるケースは多々あるが、中でも全米で最初の計画都市のひとつとして知られているコネチカット州ニューヘイブンの都市区画は「3×3」の構図が顕著であった。約300yd(274m)四方のブロックが3行3列、全体で900yd四方の街区となっている。「ニューヘイブン・グリーン」と呼ばれる教会のある緑地を中央に配したデザインは、明らかに一般の街区とは異なる様相を呈している。
次に教会建築。「十字架」の形を基礎として中央に塔の空間ができる「教会」のプランは一様に「3×3」の形となる。これは空間の中心に心柱をもつ日本の塔建築や田の字型プランに代表される住宅建築が「2×2」の様相を呈することと対照的である。一般に中央の空間が大きいため、上下左右の空間は長方形となるが、例えば世界最古の教会として知られるアルメニアのエチミアジン大聖堂は9等分のレイアウトになっている。
「四畳半」も重要な事例である。琉球畳を用いると完全な「3×3」となるこの空間は、一般的には約1800×900㎜の畳で4枚と半分。草庵風茶室の源流とされる東山銀閣の東求堂同仁斎がこの四畳半であり「茶」の文化とも関係の深い空間である。炉の切り方や出入り口の位置関係によって、「本勝手」、「逆勝手」などの名が与えられており、「3×3」から「2×4+1」への変換が、様々な「編集」を可能にすることがわかる。
その他、9-square註5)、ミステリーサークル註6)、展示用のフレーム、壁面に開いた9つの窓などがあり、水平・垂直ともに、空間デザインへの応用の可能性が感じられた。
4.2. モノのデザイン
家具、雑貨、玩具といったモノのデザインにも「正方形3×3」の多くの事例が見出された(図2)。
最も多かったのは、「9 squares」あるいは「nine squares」というキーワードで見出されるパッチワークの作品画像である。コースター、ブックカバー、枕、掛け布団など、用途は様々であるが、作品の大半は200㎜~450㎜四方のハンカチサイズであった。3×3のブロックデザインは、キルトの世界ではナインパッチ(nine patch)と呼ばれ、明暗が交互(チェッカーボード効果)になるのが定番のスタイルである。教材として最初に与えられるパターンでもあり、もっとも馴染み深い。
次に多かったのが木製の家具である。書棚、飾り棚、収納ケースを中心に「9マス」というキーワードで見つかる事例が多い。書棚の場合、高さがA4タテ(297㎜)の3倍、幅が畳の短辺(880㎜)より短く、結果、全体に縦長になる傾向が見られ、収納ケースの場合は「取り出しやすさ」への配慮からか、全体に横長になる傾向が見られた。
次はパズル・玩具で、ルービックキューブ、三目並べ(Tic-Tac-Toe)を応用した玩具、また9×9の将棋板もその延長に捉えることができた。9つのマスを用いると、要素が○と×の2通りだけだとしても、単純計算で29=512通りのパターンがあり、2×2の場合の16通りと比較して、飛躍的に複雑さが増す。三目並べも、先手必勝の単純なゲームのように見えるが、3×3の盤面で行う限り先手必勝とはならず註7)ゲーム性は高い。
数字の入力に用いる「テンキー」も特筆すべき事例である。電話とPC(電卓)では上下が逆だが、0を特殊な数字として別にすると、残りは9個。我々が扱う10進数の記号は「3×3」に配列されることで、3本の指で効率よく入力できるようになっている。上下左右斜めを意味するカーソルとしても有効で、実際にPCのテンキーはモードの切り替えによってそれを兼ねることができる。
その他は、小物入れ、箱、皿といった雑貨が大半。「3等分に折る」ことの難しさのせいか「折り紙(クラフト)」の事例は予想外に少なかった。
4.3. 情報のデザイン
絵画・グラフィック、企業のロゴ、家紋、さらに概念図など、(視覚)情報デザインの領域にも「正方形3×3」活用事例は多い(図3)。
最も有効なキーワードは「3×3 grid」だが、出現した画像の大半は数独(sudoku)の出題画像であった。数独は実際には「9×9」の行列だが、視覚的な配慮から「3×3」に背景を塗り分けたものも多く、自己相似的なグラフィックになっている。その他「3×3 grid」の事例で特筆すべきは、Anders de Flonによるフォントのデザインである。いくつか形の重複があるが、縦横の3分割だけで、アルファベット26文字と数字が識別できる程度に描き分けられることがわかる。
次に有効なキーワードは「nine squares」である。出現したものの大半は、画面を「3×3」に分割したグラフィック作品で、シンプルなタイルパターン、幾何学的抽象、組写真など、その内容は多岐にわたった。「nine squares」では他に、ロゴマーク、ピクトグラム、家紋といった幾何学的でシンプルな形のグラフィックも出現した。少数ではあるが、デザインの資料としては重要な事例を多く含んでいる。
その他、この領域で特筆すべき項目としては、曼荼羅註8)、魔方陣註9)、九数図註10)といった神秘的な意味を担う図像や、Mandal-Art註11)のような思考を視覚化した概念図が挙げられる。人間の思考は、自分あるいは神を中心に、世界を「3×3」の状態に区分けることを好むようだ。
4.4. その他
その他、弁当、菓子折り、洗剤、薬品といった類のものにも「3×3」の活用事例が多数見出された(図4)。特に「9個」という検索キーワードでは、菓子折りのパッケージが大量にヒットする。補足的に、4、6、8、9、10、12、15、16…など、数字に「個」をつけて検索したところ、9、15、16個でヒット率が高く、正方形パッケージが好まれる傾向にあることがわかった。
さて、これらは箱から出すと独立した「9つの正方形」になる。それぞれが自由に配置されると「3×3」の拡張としての様々な造形が生みだされる。調査の過程でそうした事例が見られた事も銘記しておきたい。
5. 「正方形 3×3」 の造形的可能性
この節では、見出された「正方形3×3」の事例を参考に、造形上の分類・整理を行って、それぞれの特質について考察することとしたい。
まずは「正方形3×3」の典型である「囲の字型」の造形についていくつかのパターンの可能性を考察し、次に「9つの正方形」による造形について、平面と立体の場合に分けて順に考察する。
5.1. 「囲の字型」の造形
ここで言う「囲の字型」とは、タテに3行、ヨコに3列、正方形が並ぶ形である。「塗り分ける」、いくつかの部分に「分解する」、あるいは、部分を「切り落とす」といった操作によって、外輪郭を「囲の字型」を保ったまま、様々な造形的展開を考えることができる。
5.1.1. 塗り分ける
まず、最も基本的な「塗り分け」による造形イメージを考えてみる。一般に「塗り分け」問題の「場合の数」は、公式のようなものでスマートに求まるものではないため、ここでは、1ヶ所を塗るパターンから順々に描き出した(図5)。
1ヶ所を塗るパターンは単純に考えれば9通りだが、回転や反転によって対称になるものを同一とみなせば3通りとなる。この3通りのパターンを基礎として、同様に2ヶ所塗るパターン、3ヶ所塗るパターンと順に拡張した。5ヶ所塗るパターンは、4ヶ所の場合の裏返しであり、6ヶ所以降も同様であるから、実質的に得られる塗り分けパターンは図5に示したものですべてとなる。
先行研究における「2×2」の場合は単純であったが、「3×3」になると一気に複雑さが増すことがわかる。ここでは左右反転や回転を加えたものを省略したが、それらは視覚的には明らかに異なるものであり、さらに45度の回転も含めると印象は大きく変化する註12)。「塗る」か「塗らない」かの「2値」だけでもこれだけのパターンである。色数を増やすことを前提とすれば、編集の可能性は無限に広がることがわかる。
5.1.2. 分解する
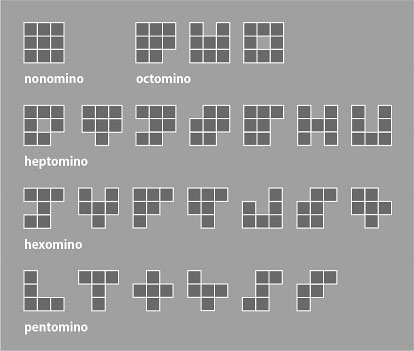
一般に「正方形を辺で連結した多角形」のことをポリオミノ註13)というが、「正方形3×3」は複数のポリオミノの分解・組合せとして考えることができる。単体はモノミノ、2連結でドミノ、3連結でトロミノ(トリオミノ)、以下テトロミノ、ペントミノ、ヘクソミノ、ヘプトミノ、オクトミノ、そして9連結でノノミノ。したがって、例えば四畳半の畳敷きは、4つのドミノ(2)と1つのモノミノ(1)の組合せとして説明することができる。 「囲の字型」を埋める組合せとしては、3つのトロミノ(3)、4つのドミノ(2)と1つのモノミノ(1)、1つのドミノ(2)と1つのヘプトミノ(7)など、様々な構成が考えられる。図6は、その一例を示したものである。
5.1.3. 切り落とす
「3×3」の外枠を保つ前提で部分を切り落とすと、オクトミノ、ヘプトミノ、ヘクソミノ、ペントミノのいずれかになり、コの字、ロの字、T字といった様々な形を切りだすことができる。図7はそれを具体的に列挙したものだが、実際には、左右を反転したものや45度回転を加えたものも視覚的には異なるグラフィックとなるため、表現のバリエーションはさらに広がりを見せる。
先に挙げた Anders de Flonによるタイプフェイス「3×3」がその典型的な応用事例であるが、「切り落とす」というシンプルな操作だけでも生成できる形状は多様になるといえる。
5.1.4. 折る(補足)
「3×3」を折りの基準にすると、「囲の字型」の展開図をもつ立体的な造形に応用することができる。しかし先に述べたとおり、今回の調査では折り紙の事例が少なく、可能性を感じるような応用事例は皆無であった。
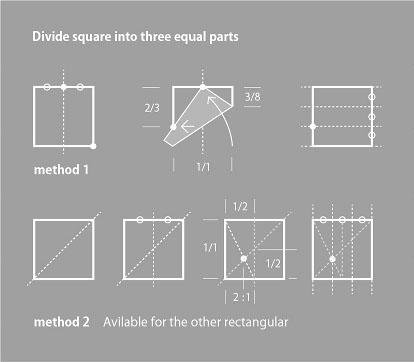
折り紙の大半は縦横斜めの「2つ折り」からはじまる註14)。図8に示すような「3つ折り」の方法は一般にはあまり知られておらず。その意味では、「3×3」の展開図を持つ折り紙には、新たな造形の可能性が残されているといえる。
5.2. 「9つの正方形」による造形
ここでは、「正方形3×3」を「9つの正方形」に分解した上で、それらを自由に再構成することを考える。「囲の字型」とはまったく異なる完成形を呈するものとなるが、「3×3」にパックされた玩具や部材の可能性を視野に入れると、9つの素材を自由に扱う場合の造形も検討に値する。
尚、一般に「図形の変換」には、移動・回転・拡大縮小の3つの操作が基本となるが、ここでは、移動と回転のみを視野に入れて考える。日常的な場面で正方形の部材に対して可能なオペレーションは移動と回転のみだからである。
以下、大きく2つ、平面的な造形と立体的な造形とに分けて考察したい。
5.2.1 平面的な造形
わずか9つの正方形だけでも、平面の構成には様々な原理が適用できる。図9はバウハウスで行われていた平面構成の演習の事例である註15)。作例からは、「単色、移動と回転のみ、重ねない」という条件のもとに構成されていること、幾何学的な基準である「辺の長さ」、「対角線の長さ」、「中心」、「対称軸」、「90度」、「45度」、「内接円」、「外接円」といったものが構成上の原理に利用されていること、また、2つをセットにしたダブルスクエア、3つのセットからできる正三角形、4つをセットにした2倍サイズの正方形といった集合単位の活用が積極的になされていることなど、様々な造形原理が読み取れる。
一般に造形教育の基礎となる「構成」は、自由度が高いほど方針が定めにくく難しい。その点、正方形には上に挙げたような幾何学的なガイドラインが多く存在するため、秩序構成の原理を見出しやすい。折り紙を「3×3」に切断するだけで簡単にできる教材だが、造形教育の基礎訓練には最適の素材であるといえる。
ちなみに、9つの正方形を辺で連結した「ノノミノ」は、回転・反転してできるものを同一と見なした場合ても、1285種類もの形状ができることが知られている。
5.2.2. 立体的な造形
立てる、並べる、重ねる、組む、吊る、張る。立体的な構成はひとつの「動詞」に注目するだけでも様々な展開が可能になる。図10は、「組む」という観点から、9つの正方形の「枠」を立体的に構成した事例である。平面的に組むノノミノ形状だけでも1285種類であるから、図はごく一部の可能性を示したものに過ぎない。
「9」という数字に構成上の必然性は見いだせないが、あえていえば、3つの正方形から「正三角柱」や「コの字型」などの安定した立体ができるという事実が重要で、それらをさらに3つ組み合わせたより大きな構造へ拡大できるという点が、「9」という数のメリットである。
先行研究の「2×2」すなわち「4つの正方形」と比較すると、単位要素が5つ増えたことになり、「5つと4つに分けて2つのものを作る」という発想も可能になる。また、5つで底のある「箱」ができることから「浮かべる」も可能になるなど、発想の契機としての「動詞」も増える。「2×2」から「3×3」への1ステップは、造形的可能性に大きな飛躍をもたらしたといえる。
尚、図のような正方形の「枠」は紐状のもので結束するだけで構造的に安定したものとなるため、遊具や玩具などにも簡単に応用できる。
6. まとめ
「囲の字型」による造形と「9つの正方形」による造形、いずれも先行研究「正方形2×2」の場合とは大きく異なる様相を呈する。
まず「囲の字型」の造形は、「2×2」の「田の字型」の造形と比較すると、偶数と奇数の違いによって中心が「点」ではなく「面」になるという構造的特徴を持つ。尖塔を中心に十字架の形をなす教会、教会を中心とした都市計画、中心に向かって再帰的な図柄を描いた「曼荼羅」など、「囲の字型」の特徴のひとつは、「特別な意味を担った中央の正方形の存在」にあるといえる。
また、周囲の要素が担う機能や相互関係についても、「2×2」の場合と比較すると飛躍的に可能性が増える。「三目並べ」や「魔方陣」は、誰もが知る最もミニマムなゲーム、あるいは数的秩序であるが、それらは自身を3倍に拡張した「将棋」や「数独」とともに、豊かなゲーム性を体現する。また、「テンキー」に見られるような9つの数字配列が「上下・左右・斜め」の概念を成立させるなど、周囲の要素が担う機能の多様性にも「囲の字型」の特徴を見出すことができる。
さらに「9つの正方形」による造形も同様で、
「2×2」から「3×3」への拡大は「4」から「9」への飛躍であり、その中間に存在する数の可能性も含むかたちで、構成原理を拡大する。「4つの正方形」からなるテトロミノが、わずか5種類しかないのに対し、ノノミノは1285種類にもなる。「9つの正方形」は、「単色、移動と回転のみ、重ねない」という厳しい制約が与えられてもなお、平面構成の課題として成立しうるだけの造形的な可能性を持っている。
「正方形3×3」は、我々をとりまく様々な空間、モノ、情報のデザインに応用されている。しかし、「3つ折り」を基礎とした折り紙の事例がほとんど無いという事実からもわかるとおり、「正方形」という身近でかつシンプルな形にも、まだまだ多くの可能性が潜んでいるのだ。「5×5」、「7×7」、と素数を追って拡大すれば、さらに興味深い事例に出会えるかもしれない。
註
1. ブルーノムナーリ,1971,正方形-その発見と展開, 美術出版社
2. 井上貢一,2012,正方形2×2 -芸術工学的「正方形」研究II-,
九州産業大学芸術学会研究報告Vol.43
3. 今和次郎(藤森照信編), 1987,考現学入門,ちくま文庫,p.399
4. Googleイメージ検索 http://www.google.com/imghp
5. 9-square:伝統的な子供の外遊び「4-square」を拡張したもの
6. ミステリーサークル:農場に突如出現する幾何学模様。当初
謎の現象として扱われたが、大半は人為的なものと判明している。
7. 19×19の盤面で行われる五目並べは禁手がなければ先手必勝
となることが知られている。
8. 曼荼羅:仏教における世界観を視覚的に表現したもの。
9. 魔方陣:n×nの正方形のマスに縦・横・斜め、いずれについても、
その合計が同じになるように数字を配したもの。
10. 九数図:古代中国の瑞祥、河図・洛書(かと・らくしょ)に
記された図。五行に由来する十数と九宮に由来する九数があり、
九数図には縦・横・斜めの総和が15になる魔方陣が描かれている。
11. Mandal-Art:今泉浩晃によって考案された発想支援ツール。
12. 井上貢一,2011,電子媒体における正方形の描画 -芸術工学的
「正方形」研究I, 九州産業大学芸術学会研究報告Vol.42
正方形を45度回転したものを見せて形を問うと大半は「ひし形」
と答える。視覚的には異なる図形として認識されている。
13. 寺垣内政一, 2009,ポリオミノの数学,広島大学教育学研究紀要
14. Densho ORIGAMI, 2010,講談社インターナショナル
15. ブルーノムナーリ前掲書p.12