音の波形
振動を数式で理解する
A sin( 2πf t + φ)
これは振動を描く基本的な式です。
t すなわち時刻をパラメータとした式で、
- A は振幅 → 音の大きさ
- f は周波数 → 音の高さ
- φ は位相差
ちなみにこの式は「純音」で、音色を特徴づける要素は存在しません。
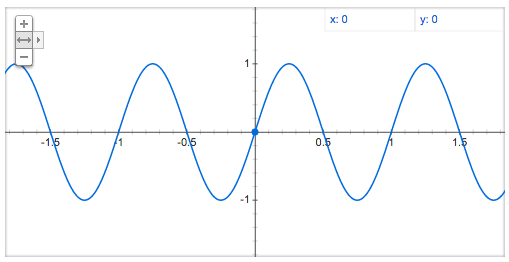
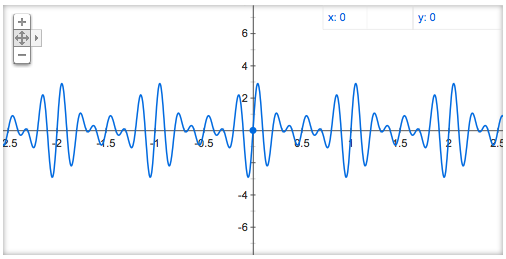
さて、2πf t という表現ですが、これは例えば f = 1 の場合、
t = 0 〜 1 で 値が 0〜 2π、つまり、1秒間で1回振動することを意味します。
右上のグラフは、1Hzの波形ということになります。
SIN関数は弧度法を使います。半径1の円の弧の長さを角度に見立てたもので、2πでちょうど一周分、つまり360°を意味します。式の括弧内の「2πf t 」は、「一秒間で f 回転」を表現するためのものです。
参考:SINだけでなぜ振動する > 単位円による三角関数の定義
参考:三角関数を使って円を描くプログラム
可聴周波数
上の図は1Hzでしたが、我々の聴覚に「音」として聞こえるのは、20Hz〜20,000Hz。上の式では、fの値が20〜20,000の範囲のものです。
例えば、
- 調弦につかう音叉の音(A4) 440Hz
- ピアノの中央ハ(C4)の音 261.6256…Hz
- 鈴虫の声 4,500Hzあたりにピーク
音声電話では帯域が300Hz~3400Hzなので、鈴虫の声は聞こえません。
倍音合成
周波数 f を基準として、その2倍の周波数 2f をもった音を2倍音といいます。また同様に3倍音・4倍音・・も考えられます。
楽器の音(シングルノート)は、基本周波数の f に加えて複数の倍音が同時に鳴ることで、その楽器特有の音色をつくっています。倍音の混ざり方で音色がかわることを波形で見てみましょう。以下、Googleのグラフ機能を使ったものです。表示倍率がそれぞれ異なっていますが、横軸xの値が 0〜1 の間でちょうど1回振動、つまり基本周波数は1であることがわかると思います。
数式からGoogleグラフへもリンクしています。数字を変えて再検索すると、波形が変化する様を直感的に確認できます。
A sin(2πft) + 0.5A sin(2π2ft)
2倍音を半分の振幅で
重ね合わせたものです。
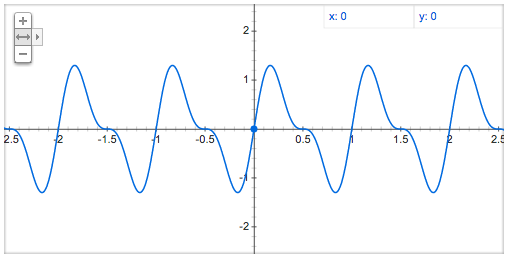
A sin(2πft) + 0.5A sin(2π3ft)
3倍音を半分の振幅で
重ね合わせたものです。
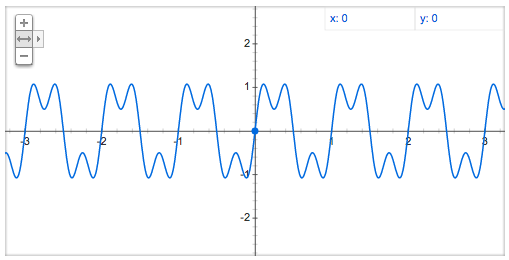
A sin(2πft) + 0.6A sin(2π2ft) + 0.3A sin(2π3ft)
2倍音を60%、3倍音を30%の振幅で
重ね合わせたものです。
音のハモり
ハモるとは、物理的には、高さ(基本周波数)の異なる複数の音で、その整数次倍音に共通の周波数が含まれる場合に成立します。別の言い方をすれば、それらの周波数比が簡単な整数比になることを意味します。
例えば、5度の音程「ド」と「ソ」では、「ド」の3倍音と「ソ」の2倍音が同じ周波数の音になります。言い換えれば、ドとソの基本周波数の比は2:3という簡単な整数比になっています。
また例えば、長3度の音程「ド」と「ミ」の周波数比は4:5なので、いわゆるメジャートライアド「ド」「ミ」「ソ」は、4:5:6という比率になり、可聴周波数帯の範囲に複数の共通する倍音を持つことになります。
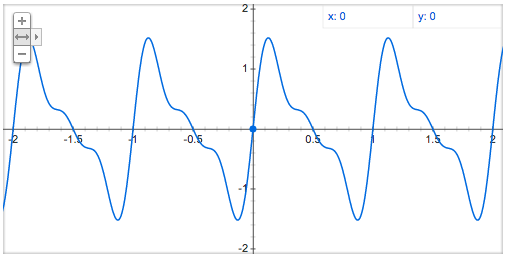
A sin(2π4ft) + A sin(2π5ft) + A sin(2π6ft)
周波数比4:5:6の3音の重ね合わせ。
音に周期性が見られます。
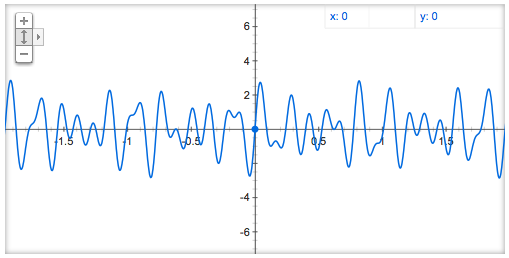
A sin(2π4ft) + A sin(2π5.1ft) + A sin(2π7.7ft)
複雑な比率の音の組み合わせ。
当然ですが、周期性がなくなります。
ちなみに完全8度、すなわち1オクターブの音程は1:2ですから、「ド」の音を3倍して1オクターブ下げれば「ソ」の音が得られ、その「ソ」を3倍して1オクターブ下げれば「レ」が得られます。このようにして得られた音律(音程調律)は「純正律」と呼ばれるもので、倍音のうなりを伴わない、きれいな和音が得られます。
一方、1オクターブを単純に等比的に分解する調律を「平均律」といいます。移調・転調に対して、相対的な周波数比が保たれるので、現代の音楽では平均律の楽器(ギターが典型)を使うのが普通ですが、純正律のような綺麗な和声は得られません(ちなみにデジタルキーボードには、純正律・ピタゴラス音律・平均律などの音律の変更ができる機種もあります)。