第1回 ガイダンス
CONTENTS
はじめに
現代社会におけるデータサイエンスの位置付け
データサイエンス(Data Science)とは、データそのものの性質やデータを取り扱う手法を研究する科学全般を指す言葉で、統計学、機械学習、データマイニング、可視化・・など、様々な分野を包括する概念です。
数値や文字(カテゴリ)として得られるデータを統計的手法や機械学習(近年の AI の技術ベース)などを用いて分析・処理することによって、世界に潜む様々な物事の関係(モデル)を見出す科学であるとも言えます。
関連する諸分野との関係を図で表すと以下のようになります。
GoogleImage:Data Science Machine Learning AI
これが正しい・・という図を書くことはできません。作図する人の立場や説明の手順によって、それぞれの包含関係は変わるので、ざっくり位置関係を把握すれば十分ではないかと思います。
コンピュータが可能にしたこと
今日の AI技術 もデータサイエンスも「大量のデータから最適解を見出す」という点では共通しています。これまで、数理的な問題解決には、解析的な方法で数式を解いて答えを出す・・という学び方をしてきたと思いますが、コンピュータが使える今日では「力ずくで最適解に近づく」ということが可能になりました。
数学の問題は、計算によって綺麗な整数解が得られるように作られていますが、現実の問題はそうではありません。で、実際のモノ作りの現場では、実用上「ミリの単位までの数字で十分」ということがあります。
今日の数理の世界では、コンピュータの登場によって従来とは異なる発想が可能になっている・・という事実を確認しておきましょう。
データサイエンスにできること
- 判別:情報の判断・仕分け・検索、音声・画像の認識、異常検知など
- 予測:数値予測、ニーズ・意図予測、マッチングなど
- 実行:作業の自動化、表現生成、行動の最適化など
データサイエンスの限界
データからわかるのは過去から現在までことです。データの活用は、未来の予測や目標達成のための「最適化」には効果的かもしれませんが、生物の社会のような複雑な系の未来を予測することや「創発」的なデザインには限界があります。
人は未知のものにニーズを抱くことはありません。つまり過去のデータからニーズだけ探っていてもダメ・・ということです。デザインを志すみなさんには、データサイエンスの威力を感じつつも、若干引きで眺める姿勢が必要です。
関連事項
一般にデータサイエンスの教科書では、データを扱う人の心構えとして、以下のような事項が記載されていますが、みなさんは、すでにソーシャルデザイン演習・応用演習、また学科サイトの日常的な運用において、このあたりは学習済みなので、この演習では省略します。
- 情報倫理
- 情報セキュリティー
- 著作権 と CreativeCommons・Copyleft について
本演習への取り組み姿勢について
本演習では、サンプルや受講生の成果をWeb上に公開することから、単にソースをコピペするだけでも「やったふり」ができてしまいますが、物事を「オープン・ファースト」で考えるという前提のもとで、「パクる」と「真似る」の違いを踏まえて、ポジティブに取り組む(自分自身でコードを書き換えていろいろ試してみる)ことを期待します。
- パクる:単にオリジナルを移動・複製して所有すること(盗むと同義)
「パクる」だけでは何の学びにもなりません。 - 真似る:しくみを理解した上で、自分の力で同様のものを作り出すこと
「真似る」は「学ぶ」の語源とも言われる行為。子供は大人のやることを真似することで生きる術を身につけます。同様に、多くの学びは、憧れや理想を契機として、誰かの行為や創造物を真似ることからはじまります。
インターネットの普及によって、自由な情報共有を前提としたオープンな仕組みが世界を変えようとしています。誰かの情報があなたの学びに役立つと同時に、あなたが公開する情報が誰かの役に立っています。
データの取り扱い
データとは
データ(Data)とは、一般に情報伝達、解釈、処理を目的として符号化された情報(与件・所与)のことです。
- 日本工業規格:X0001 情報処理用語-基本用語
情報の表現であって、伝達、解釈または処理に適するように形式化され、 再度情報として解釈できるもの
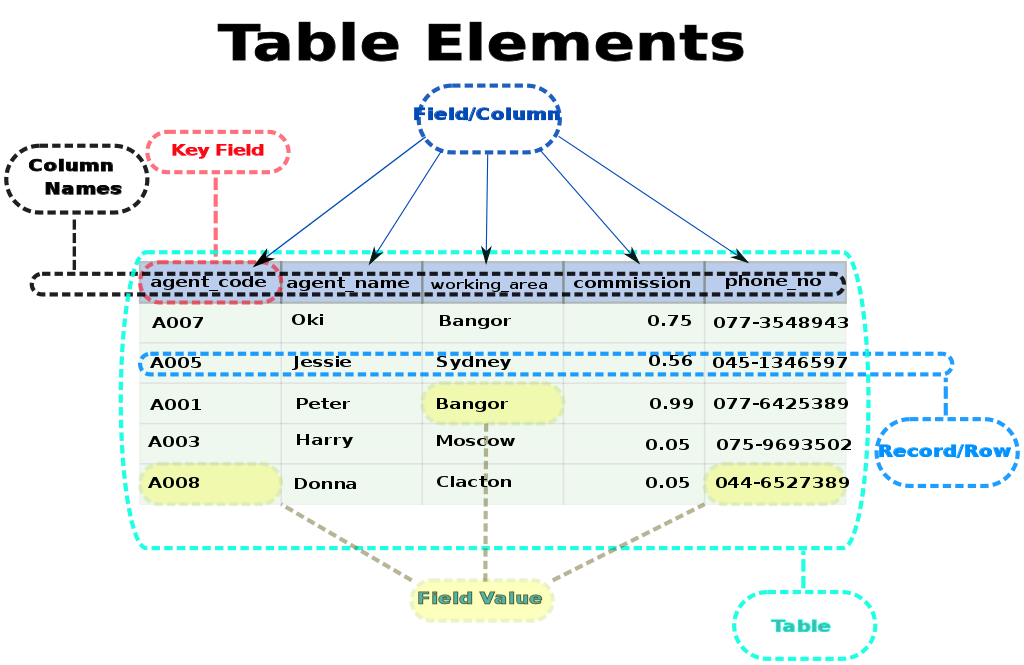
データファイルの基本構造
データファイルは一般に2次元の表形式で与えられます。以下の用語を理解しておくことが必要です。
- テーブル / Table(表):通常1つのファイル
- レコード / Row(行):1件分のデータセット
- フィールド / Column(列):特定項目に関するデータセット
表の先頭行にはフィールド名(項目見出し)が並ぶのが一般的です。
出典:https://commons.wikimedia.org/wiki/File:Table_Elements.svg
様々なデータファイル形式
- CSV(.csv)
CSV(Comma-Separated Values)は、表形式のデータ等でフィールド項目をカンマ [ , ] で区切ったテキストデータです。データ交換用の標準形式として、多くのスプレッドシートやデータベースソフトで活用されています。ちなみに、タブで区切られたものをTSV(Tab-Separated Values)、半角スペースで区切られたものを Space-Separated Values といいます。 - EXCEL(.xlsx)
みなさんお馴染み、スプレッドシートの代表的なデータ形式です。データとして読ませること前提とした Excelシートの場合、表の先頭行がフィールド項目名になるようにしましょう(視覚的な配慮のための余白や、大見出し等は省略してシンプルな表にします)。 - JSON(.json)
Webアプリケーションの世界でよく利用される形式です。興味のある方は、以下のページをご参照ください。
JavaScript Object Notation >JSON
オープンデータについて
オープンデータとは、著作権、特許などの制限なしで、全ての人が自由に利用・再掲載できるデータ(またその考え方)です。興味のある方は、以下のページをご参照ください。
- 詳細はこちら >OpenData
演習1|Spreadsheet の基礎
はじめに
- GoogleDrive のマイドライブ内に、当演習授業用のフォルダを DataScience 等の名称で作成してください。
- 今後の毎回の演習の成果は、そのフォルダ内に置いた上で、学科サイト上の個人ページからリンク共有することが前提となります。
作業準備
- GoogleDrive > マイドライブ > DataScience フォルダの中で右クリック、新規の Spreadsheet を作成してください。
- シートの表題を「スプレッドシートの基礎」などとして下さい。
- スプレッドシートの入門体験の意味で、シート上に「時間割」を作成する演習を行います。以下を参考に、自分にとって見やすい時間割を作成して下さい。
事例:スプレッドシートの基礎
注)コピペすれば一瞬でできますが・・自分で操作して使い慣れて下さい。
Spreadsheet の基本操作体験
以下の事項を確認して下さい。
- 表は左端上( A1)から埋めて下さい。データとして利用する場合は、見やすくするための行・列余白は逆に邪魔になります。
- セルの指定( A1 , C5 など)方法を確認して下さい。
- 行・列の追加挿入、複製などの基本操作を確認して下さい。
- オートフィル(曜日や連番数字は半自動的に入力可)を確認して下さい。
- SUM( ), COUNTA( ) などの関数や計算式の書き方を確認して下さい。
- 必要に応じて、罫線・背景色・文字色等で表を見やすくして下さい。
- 出来上がったシートをCSV形式でダウンロードして、テキストエディタ等で、その中身を確認して下さい。
学科サイトで学科サイトにリンク掲載
- 1. Spreadsheet を開いた状態で、右上の「共有」をクリック
- 2. 共有設定を変更して、以下のように表示される状態にします。
このリンクを知っているインターネット上の全員が閲覧できます。
- 3. 「リンクをコピー」をクリックして、そのアドレスを、以下の形式で、学科サイトにリンク掲載して下さい。
-[[スプレッドシートの基礎>https://docs.google.com/spreadsheets/・・=sharing]]
- 4. 以下のようになればOKです。
https://design.kyusan-u.ac.jp/socialdesign/?JohnSmith/DataScience
APPENDIX
皆さんは、数学の世界を分類する代数 幾何 解析という用語を覚えていますか。学問領域を完全に線引きして区別することはできないのですが、それでも分類用語を知っておくことは「今、自分は何を学んでいるのか」を理解する一助となります。データサイエンスの世界も同様、様々な 関連用語 をざっくりと把握するだけでも、全体像が把握しやすくなります。
以下の区分も、知っていると世界がさらに見えやすくなります。
決定論と確率論
数理の世界には、決定論的なアプローチと、確率論的なアプローチの2つがあります。たばこの煙に例えると、たばこの先から一直線に上昇している部分の粒子の位置は、時刻 t を変数とした数式で決定論的に記述されますが、天井に拡散した粒子のふるまいは、確率論的にしか記述できません。ちなみに、その中間にある煙の「乱れそめ」の部分は「カオス理論」の対象となりあす。
- 「落下する物体の位置」のように数式で記述できる事象は決定論の対象
- 「臨床試験の結果」のように統計的に扱う事象は確率論の対象
線形と非線形
- 比例関係にあるものが「線形」
線形な漸化式の例: \(X_{n+1} = a \cdot X_n + b\) - 比例関係にないもの、例えば、一旦下がってまた上がるようなふるまい、あるいは、予測のつかないふるまいをするものが「非線形」
非線形な漸化式の例: \( X_{n+1} = a \cdot X_n(1 - X_n) \)- 0 < a < 1 のとき:一定値 X = 0 に収束
- 1 < a < 3 のとき:一定値 1 - 1 / a に収束
- 3 < a < 3.57… のとき:振動
- 3.57… < a のとき:予測不能な複雑な動き(カオス的領域)
- 実際の計算とグラフ化:JupyterNotebook
- ちなみに、生き物の成長は非線形的で最後は飽和状態