逆関数法
Inversion Method
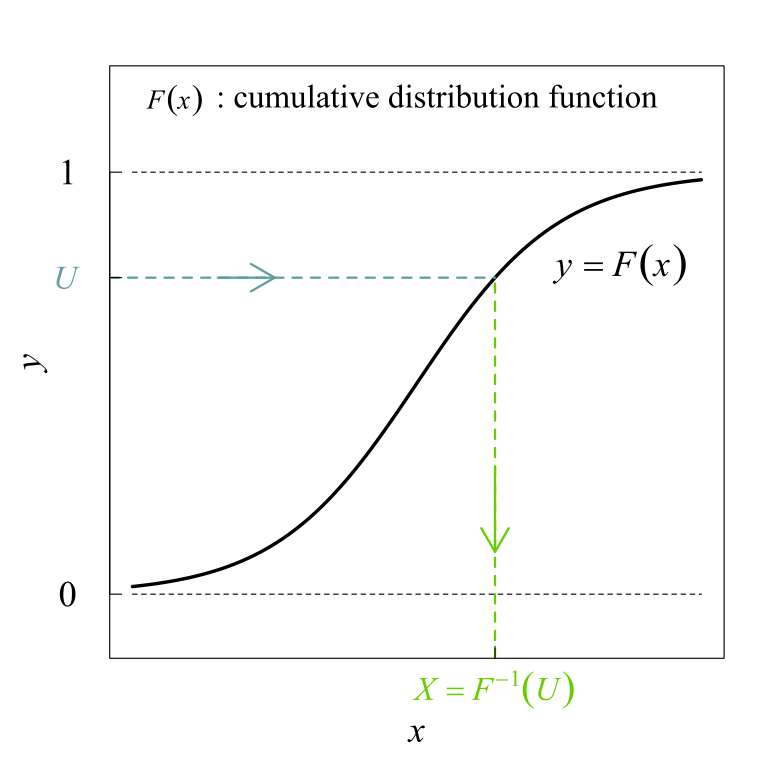
逆関数法（inversion method）とは、累積分布関数の逆関数を用いて、様々な分布に従う確率変数を生成する手法のことです。コンピュータを用いたシミュレーションでは、プログラム言語に標準的に用意された「標準一様分布に従う乱数 [ 0,1 )」にこの方法を適用して、指数分布やポアソン分布に従う乱数を生成します。
Source：Wikimedia Commons File:Inversion method.svg
原理
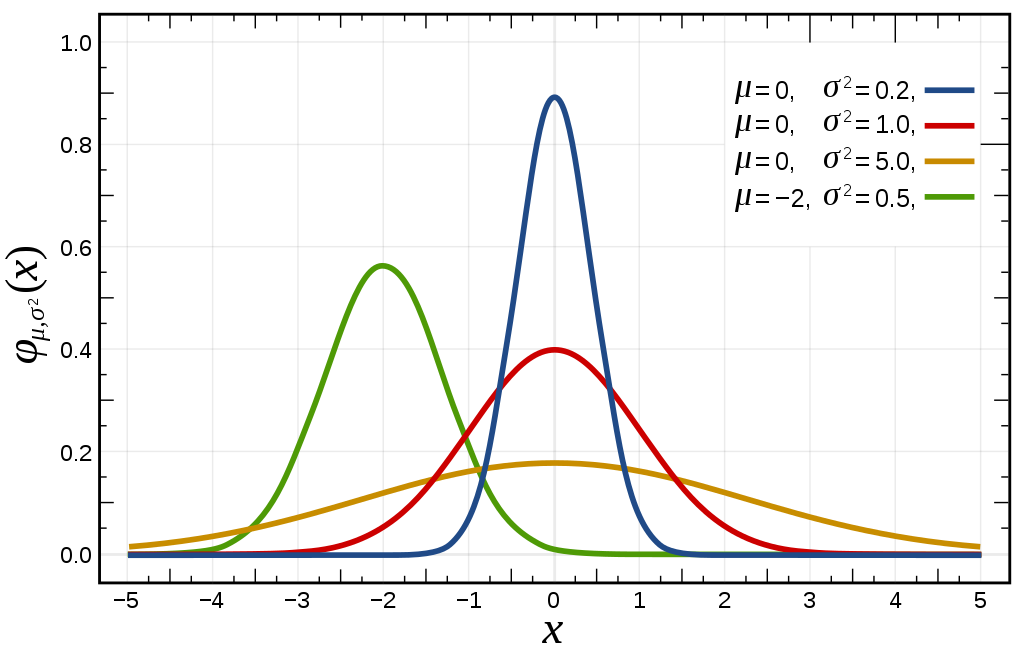
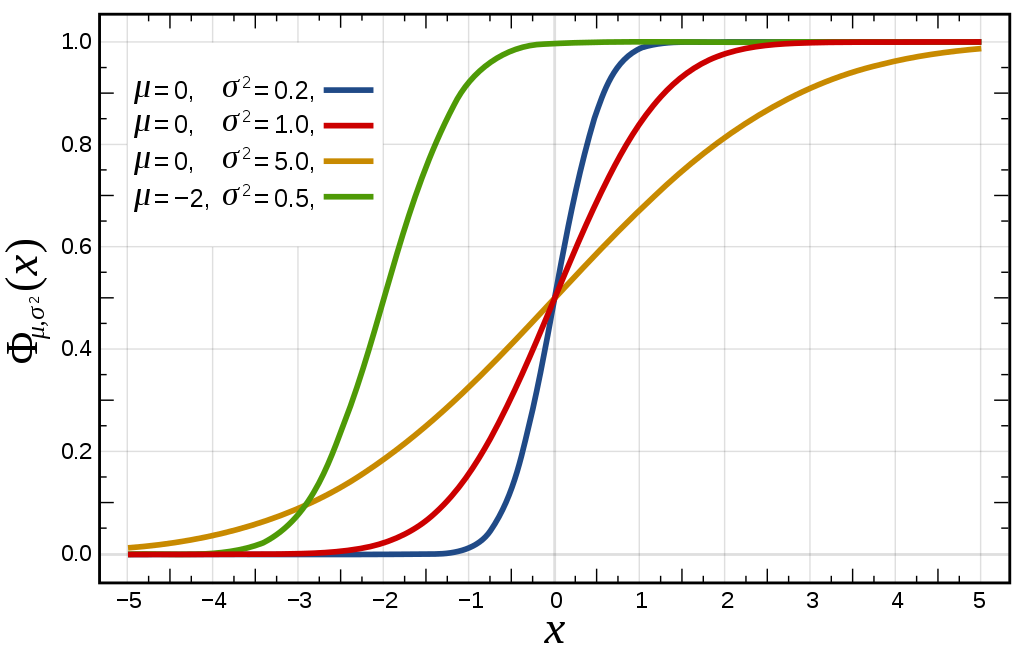
連続型の確率密度関数 \( f(x) \) を \(-\infty\) から x までを定積分すると、累積分布関数 \( F(x) \) が得られます。
 |  |
| 確率密度関数 f(x) | 累積分布関数 F(x) |
Wikimedia Commons： Normal Distribution PDF.svg , Normal Distribution CDF.svg
\( F(x) \) は 0.0 〜 1.0 まで単調に増加するのが一般的で、 \( f(x) \) において、分布の山にあたる部分では、 \( F(x) \) は急激な上昇カーブを描き、分布の裾野にあたる部分では、 \( F(x) \) はゆっくりと上昇します。
関数を逆向きに見て、y軸側から標準一様乱数（0.0 〜 1.0）を「カーブにぶつける」とすれば、急激な上昇をする箇所（もとの分布では山にあたる部分）の範囲が広くて「当たりやすく」、結果、x軸上の当該部分付近で乱数の分布が密に（分布の山に）なります。つまり、この x は
\( f(x) \)
に従う乱数として使える・・というのが直感的な説明です。
事例｜指数乱数
事例として、指数分布 \(X 〜 E_x(λ)\) に従う乱数の生成について概説します。
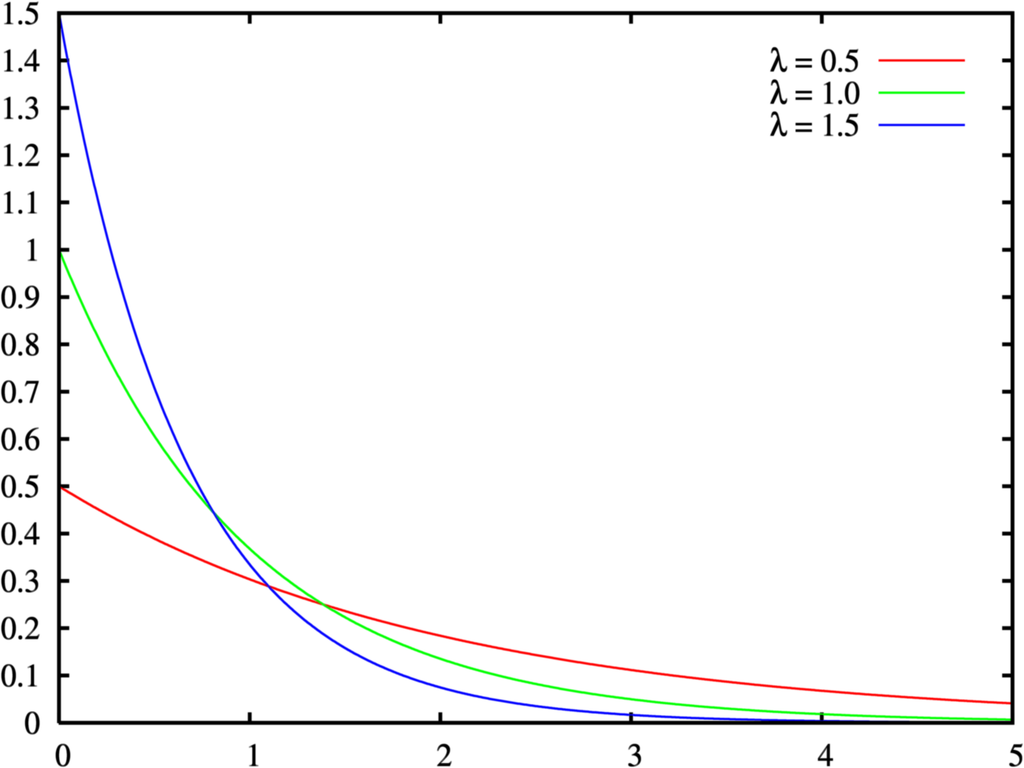
指数分布の確率密度関数は、右のようなグラフで、これを関数式で書くと以下のようになります。
Source：Wikimedia Commons File:Exponential distribution pdf.png
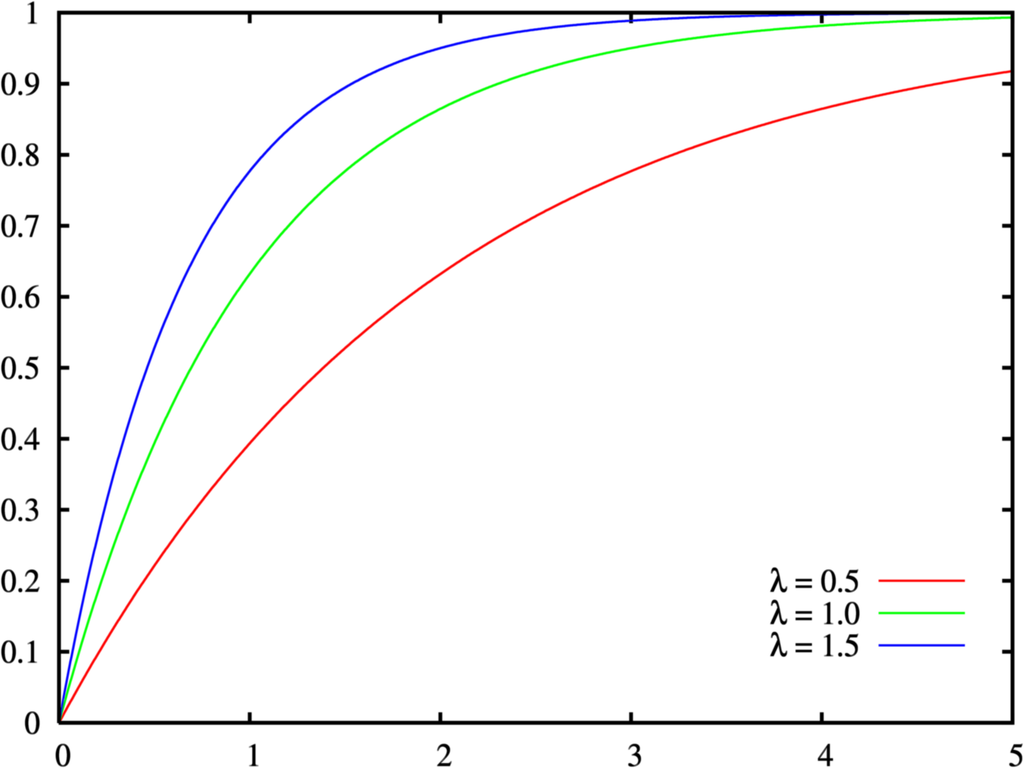
指数分布の累積分布関数は、右のようなグラフで、これを関数式で書くと以下のようになります。
Source：Wikimedia Commons File:Exponential distribution cdf.png
この逆関数は、 \( F^{-1}(x) = -\frac{1}{λ} \ln(1-y) \) で、 \(X = -\frac{1}{λ} \ln(1-U) \) となります。 \(1-U\) は、実質的に \(U\) と同じになるため、高速化のためにこれを簡略化して、以下の式が得られます。
註）：Uは、標準一様分布の確率変数で、0.0 〜 1.0 の値を取ります。
註）：ln は e = 2.71828182...を底とする 自然対数（natural logarithm）です。
指数分布のパラメータ λ は、確率変数 X の 期待値 （1 / λ）の逆数にあたるもので、直感的にわかりにくいので、期待値を \(μ = 1/λ\) として、以下のように書く方がわかりやすいかもしれません。
指数乱数のプログラム例
以下、Python で記述した例です。
GitHub：InversionMethod.ipynb
CumulativeDistribution.png
ExponentialDistribution.png
InversionMethod.png
