コンピュータ・グラフィックスには、造形的規則と生成パラメータを手続きとして与えて、プログラムによって自動的に描画させる・・というタイプのものがあります。Photoshopのフィルターにある「雲模様」もそうした「自動生成」するタイプのCGです。
ここでは、その事例をC言語風の書き方とともに紹介します。実際にプログラムを書いて動かすには、Processingなどのグラフィックスの描画ができるプログラミング環境を準備する必要があります。
for( x=0; x<width; x=x+step ){
/*ここに「描画命令」を記述*/;
}
for( y=0; y<height; y=y+step ){
for( x=0; x<width; x=x+step ){
/*ここに「描画命令」を記述*/;
}
}
描画空間の座標(x,y,z)を、高次の多項式や三角関数を用いてパラメトリックに表現すると、複雑な幾何学模様をつくることができます。縦方向の振動と 横方向の振動が合成してできるリサージュ図形などがその典型です。
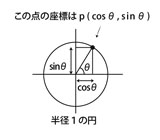
x ← cos θ
y ← sin θ
座標 ( x, y )に点を打つ(画素に色を付ける)
θをわずかに増やす
以上を繰り返すと画面に円図形が描かれます。
for( th=0; th<2*PI; th=th+0.01 ){
x = R * cos(th);
y = R * sin(th);
PIXEL( x+CX, CY-y );
}
PI:円周率 R:半径 CX,CY:画面の中心、PIXEL( )は点を打つ関数
for( th=0; th<2*PI; th=th+0.01 ){
x = R * cos( FX * th );
y = R * sin( FY * th );
PIXEL( x+CX, CY-y );
}
FX, FY はそれぞれ横方向・縦方向の振動数
x = R1*cos(FX1*th) + R2*cos(FX2*th) + R3*cos・・
のように複数の振動が重ね合わさった状態
for( th=0; th<2*PI; th=th+0.01 ){
r = R * sin( F * th );
x = r * cos(th);
y = r * sin(th);
PIXEL( x+CX, CY-y );
}
k ← n を 3 で割った余り(剰余)
k の値を色の値として図形を描く
n ← n + 1
以上を繰り返すと、画面には
012012012012・・と周期的な
色の変化が現れます。
for( y=0; y<height; y=y+step ){
for( x=0; x<width; x=x+step ){
c = ( x * y * y ) % 256;
SetPixel(hDC,x,y,RGB(c,c,c));
}
}
数式がつくる形は規則的で冷たいという印象を受ける
そのような場合は
A ← A × ( 1 + 乱数(1より小さな範囲の) )
などとして、計算結果 ( A ) にわずかにランダムな要素を混ぜる
ことで、変化を加えることができます。
一様乱数の生成例
x = rand() % 640; /* 0-639 */ y = rand() % 200 + 140; /* 140-339 */
※ % は剰余計算(割った余りを求める)
正規乱数の生成例
s = 0.0; for( i=0; i<12; i++) s = s + RAND(); s = s - 6; /* s : 平均0 標準偏差1の正規乱数 */
RAND( )は、[0.0 , 1.0 ) の正規乱数生成
部分の形が全体の縮小形になっているというような「自己相似性」をもつ図形をフラクタル図形といいます。樹木・雲模様・海岸線の形状など、いずれの形も、 基本となる「図形を描く」プログラムをその図形の一部を描く部分に再帰的に利用することで生成することができます。例えば「一本の幹の先端に二本の枝を描 く」というプログラムを、その枝を描く部分に適用すれば、枝の先端から二本の子枝ができる。これを子枝・孫枝:と繰り返せば、枝の生い茂る木ができるとい うしくみです。
フラクタル図形は、きっかけとなる手順やデータが単純であっても、できあがる全体は非常に複雑で、またわずかな初期値の違いが最終的な結果を大きく左右す るために、最終的なイメージは予測がつけにくい存在です。
このようなシステムを一般に「複雑系(Complex System)」と言います、実は、我々生命体を含む多くの自然現象がそのようなふるまいをしているのです。
要素単位で見れば単純な規則でも、複数の要素が影響しあうと非常に複雑になります。膨大な計算を必要とするものであり、コンピュータの存在無くしては、こ のようなイメージには出会えません。
生成規則の1例
親の世代の左と右が01または10のとき子は1となる
逆に00または11のときは子は0となる
1行目(ご先祖) 00001000010000100
2行目(2代目) 00010100101001010
3行目(3代目) 00101011000110001
4行目(4代目) 01000011101111010
: :
この01並びを模様として描くと
複雑な3角形のパターンができます。
生成規則の1例
『枝を描く』という命令が
1)枝を描くと同時に
2) 先端左に小『枝を描く』
3) 先端右に小『枝を描く』
という処理内容であれば、
枝が小枝を、小枝が孫枝を描くことになり(一定限度でストップ)、
これを幹を最初の枝としてスタートすれば、
結果的に右図のような樹形になります。
縦を虚数軸、横を実数軸とした「複素平面」を前提とした造形です。
Zn+1 ← Zn^2 + C n ← n + 1
この計算を Z0 = 0 から一定回数繰り返した場合(例えば100回程度)、定数Cの値によって、域外へ発散する場合と、そうでない場合があります。
複素平面上の縦横とも ±2の範囲で、すべてのC( a + bi )について、上記の計算で発散するか否かを調べ、発散しない場合のCの点(a,b)を黒として塗り分けると、右図のような図形になります。
実数の世界では、1未満の数字は2乗し続けると0に、1を超える数字を2乗し続けるとあっという間に発散するのですが、ZとCは複素数なので、このような複雑な状況になる・・・非常に不思議な現象です。
マンデルブロ集合と同様、縦を虚数軸、横を実数軸とした「複素平面」を前提とした造形です。同じ計算式ですが、ジュリア集合では Zの初期値を動かします。
Zn+1 ← Zn^2 + C n ← n + 1
一定のCの値について、 様々なZ0( a + bi )を初期値として計算繰り返すと、Z0の値によって発散する場合と、発散しない場合があり、発散しない場合のZ0の点(a,b)を黒として塗り分けると、右図のような複雑な図形になります。
初期位置
P0 ( x0 , y0 )を与えて
xn+1 ← f( xn,yn,a) yn+1 ← g(xn,yn,a) n ← n+1
という漸化式を繰り返すと、計算式の与え方次第で、
1.収束 2.振動 3.発散 4.非周期的振動のいずれかになります。この4番目の場合が、カオス図形(うごめく秩序)です。
ページを独立させました。> ComplexSystem