論理回路
論理回路(logic circuit)とは、論理演算を行う電子回路のことで、0 / 1、true / false を、電圧の高低や、電流の方向、位相差、パルス時間の長短、などで表現するかたちで、一定の論理演算が行えるようにその仕組みを実装したものです。
組み合わせ回路
現在の入力のみで出力が決まる回路で、以下のような基本回路があります。
NOT回路
OR回路
| Symbol | In1 | In2 | Out |
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
AND回路
| Symbol | In1 | In2 | Out |
|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
XOR ( Exclucive OR ) 回路
| Symbol | In1 | In2 | Out |
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR回路
| Symbol | In1 | In2 | Out |
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
NAND回路
| Symbol | In1 | In2 | Out |
|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
組み合わせ回路の構成例
半加算器
2進数の同士の加算における1桁目の加算を担当する回路で、XORゲートとANDゲートを使って構成することができます。
| Circuit | In1 | In2 | S | C |
|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
- 1桁目の計算(Sum:和)は XORゲートの出力を利用
- 2桁目(Carry:桁上がり)は ANDゲートの出力を利用
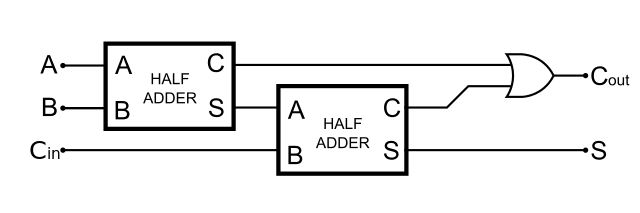
全加算器
2進数の同士の加算における2桁目以降の加算を担当する回路で、様々な構成例があります。ここでは、基本回路で組んだ例と、半加算器を一つのユニットとして組んだ例、2つの回路図を紹介します。
| Circuit | C_in | In1 | In2 | S | C_out |

 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
加算回路(複数桁)
1桁目に半加算器、2桁目から先に全加算器を並べて、下の桁の C_out(桁上がり)の出力を、当該桁の C_in に入力することで、複数桁に対応した加算回路ができあがります。
2進数同士の加算は、以下のようなイメージになります。
以下、1110 + 101 = 10011(14+5 = 19)の計算です。
| 1 | 1 | | | | ← 繰り上がり |
| | 1 | 1 | 1 | 0 | 14 + 5 |
| +) | | | 1 | 0 | 1 |
順序回路
順序回路は過去の内部状態と今の入力信号とで出力が決まる回路で、ループ回路によって内部に状態を保持します。コンピュータの主記憶装置やキャッシュメモリ、レジスタを構成する基本回路の一つです。
Flip-Flop
フリップフロップは、1ビットの情報を保持する(記憶する)ことができる論理回路で、現在の出力を入力側へフィードバックすることで情報を保持します。
| Circuit | S | R | Q |
|
| 0 | 0 | 保持 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 禁止 |
- S(Set)とR(Reset)の2つの入力を持つ SRフリップフロップ回路です。
- S に1が入ると Not S = 0 が上のNAND に入って Qが1になり、そのフィードバックが下の NAND に入ることで、Not Q が 0 になります。
- R に1が入ると Not R = 0 が下の NAND に入って Not Q が1になり、そのフィードバックが上の NAND に入ることで Q が 0 になります。
- 入力がいずれも0の状態(上にも下にも Not 0 = 1 が流れている)のがアイドリング状態で、現状を維持します。
- S と R が同時に入った場合の動作は不定なので、一般に禁止されます。