正方形研究・序説
-芸術工学的"かたち"の理解-
Study on "SQUARES" - Understanding "Figures" in field of design
はじめに
我々をとりまく環境には、正方形が豊富にある。正方形の空間、正方形の家具、正方形の絵や図表、そして画面の最小単位である画素にいたるまで、あらゆる時と場所にそれは存在する。
しかし、この形はあまりにも日常的で、理解が簡単にできることから、「なぜ正方形なのか」という問いが発せられることは少ない。
筆者がこの研究ノートを執筆しようと思ったきっかけのひとつは、自分自身がまず「正方形」という形に魅かれる理由を様々な角度から考察してみたいと考えたことにある。筆者はいわゆるアーティストではないが、デザイン研究のために実験的作品を作る際には、常に正方形のフォーマットを使ってきた註1)。それにはいくつかの理由がある。「縦横比をどうするか」という制作初期の難問を省略できる。「幅・高さ」ではなく「サイズ」という一つの変数で済む。どんな展示空間にも合わせやすい。セットで展示する際に様々な配列が試せる。車に積み込む時に、縦か横かで迷う必要がない。要するに「楽」なのである。
もうひとつのきっかけは、近年飛躍的に便利になったWeb上の画像検索の可能性に触発されたことにある。例えばGoogleの画像検索で「9 x 9」と入力して検索すると、数独、9cm × 9cmの卓上カレンダー、碁盤の目など、様々な正方形が現れる註2)。実際に1x1、2x2と順に試せば、世の中にある正方形がすべて閲覧できるのではないだろうか。これだけの数の正方形を眺めていれば、何か新しい発見があるかもしれない。
風呂敷、折り紙、四畳半。日本には正方形に関わる知恵が豊富にある。正方形という切り口からデザインの可能性を模索してみたい。
1.研究の目的と背景
本研究の目的は、「正方形」という形に着目し、その定義や性質を確認するとともに、様々な分野へのデザイン応用、また造形教育の活性化に資すべく、その形のもつ可能性について、関連諸学の知見を整理することにある。
一般にデザインの教科書は、色とかたちの二部構成、点・線・面・立体・動きといった「次元」を基準にした構成、また秩序・分割・バランス・リズムなどの構成原理を基準に章立てしたものが多い。例えばバウハウス叢書No.2、P.クレー(1879-1940)のノート「教育スケッチブック」註3)では、線と構造・次元と平衡・引力・運動エネルギーの四部構成、同No.9、W.カンディンスキー(1866-1944)の「点と線から面へ」註4)では、序論・点・線・地平面という構成である。また、近年の著作で評価の高いK.イーラムの「Balance in Design」註5)では、第四章に長方形についての詳細な記述があるのだが、例えば、第一章「円」、第二章「正方形」…のように「形」という切り口からデザインを総合的に捉えようとする試みは、次節で触れるブルーノ・ムナーリ(1907-1998)のもの以外には見当たらない。
本稿ではそうした背景をふまえ、まず「形」を総合的に捉えることからデザインの領域へとアプローチする。形には、直線、曲線、正方形を含む多角形、円を含む楕円、さらにその複合まで様々なものがあるが、本稿では、その優れた対称性と、Web上の画像資源の豊富さ、そして我々日本人の経験を生かすべく「正方形」に注目する。
空間、モノ、情報、あらゆる場面に正方形は現れる。それらのアウトラインを概観して、「正方形」研究の序説とする。
2.「正方形」に関する先行研究
ここでは、「正方形」研究の先行事例となる書籍、論文、Web上の記事について、キーワード検索を行った結果を報告する。
2.1.書籍
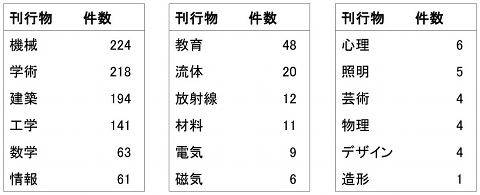
Amazon.co.jpで「正方形」をタイトルに含む和書を検索すると、わずか8件のヒットという結果になる(2009.09.17)。その中で、デザイン・造形的な観点から正方形に言及したものを抽出すると、右下表の4件に絞られ、さらに、主題に「正方形」という文字を含むものに絞れば、ブルーノ・ムナーリの本が唯一の存在となる。
ブルーノ・ムナーリによる「円+正方形-その発見と展開」はそれ自体が15cm四方の2冊組で、そのひとつに「正方形-その発見と展開」(IL QUADRATO)と題がついている。この本には目次がない。すべての項目がアルファベット順に掲載されており、ムナーリ自身がその前書きで「索引の必要はない」といっている点もユニークである。ムナーリによれば、正方形は「完全な一つの空間概念の極限の集約」であり、「充実した精神の象徴性の秩序を表現」している。「囲い、家、村の概念を意味し」、「美術的な構築をするに当たって調和ある骨組みを与え」、またチェスやダイスなど古くからある「遊びの因」にもなっている。
AGORA 註6)の平面図にはじまり、WANG HSI-CHIH 註7)の草書・楷書体まで、建築物、美術作品、日用品、文字、さらに正方形に関わる幾何学や抽象概念、詩に至るまで、全170項目に言及した貴重な資料である。
2.2.論文
CiNii(cinii.ac.jp:論文情報ナビゲータ)の検索で「正方形」をタイトルに含む論文を検索すると、1243件の論文がヒットする(2009.09.17時点)。右下の表は、それを刊行物のキーワードと合わせて検索した結果である。例えば、論文名:「正方形」、刊行物:「デザイン」とセットにして検索すると、「デザイン学研究」などに掲載された「正方形」をタイトルにもつ論文がヒットする。
この結果をみると、芸術・デザイン・造形分野では、正方形そのものを正面から扱った論文が少ないことがわかる。しかし数学の分野では作図に関する研究や折り紙に関する研究、さらに「日本人は正方形が好き-絵画に見る比率の違い-」、「正方形が好きな日本文化と数学」(いずれも渡辺信氏 東海大学海洋学部)といった論文もあり、注目すべき先行研究が多い分野であるといえる。
ちなみに機械工学分野では、流体に関わる正方形Cavity(空洞)、放射線分野では正方形照射野、電気・磁気分野では正方形コイルなど、物理現象という観点から正方形形状を扱った論文が多い。
2.3.Web上の資源
Web上には「正方形」をタイトルに含むページが約386,000件あるが、研究の初期段階という意味では、やはり群衆の叡智であるWikipediaの資料価値が高い。信頼性には賛否あるにせよ、そこにはムナーリの項目をはるかに上回る正方形関連情報が存在する。またWikimedia CommonsにはGeometry、Urban squares、Tool、Shapeといった区分があり、多くの正方形関連画像がPDあるいはCC 註8)として提供されている。
3.正方形概説
この節では、正方形というものについて、まずその言葉の定義、そして数学的な記述、さらに具体的な作図について概説したい。
3.1.正方形の定義
辞書によれば正方形とは「(1)正四角形の通称、(2)四つの辺・四つの内角が、それぞれ等しい四辺形」とある註9)。参考までに加えると、「正方」は「(1)真四角。正方形。(2)正しいこと。方正」、さらに「方形」は「四角(しかく)。四角形」である。
数学的には「四辺がすべて等しく、四角がすべて等しい四角形」、「長方形かつ菱形」、「隣り合う辺の長さが等しい長方形」、「対角線の長さが等しい菱形」、など様々な説明が可能である。
図形の系統的には、一般の四角形から進化して、一組の対辺が平行になると台形、さらにもう一組の対辺が平行になると平行四辺形になる。次に角をすべて等しく(直角に)した長方形、あるいは、辺の長さをすべて等しくした菱形へと進化し、その後、長方形の辺の長さを等しくするものとして、あるいは菱形の角をすべて等しくするものとして、最終的に正方形へと進化する。四角形の中では、最も対称性に優れた形である。
3.2.数学的記述
正方形は4本の非連続な直線からなる形であり、ひとつの条件式で記述することが難しい。よって、一般に以下のような点の集合として表現する。
{ ( x , y ) | -r ≦ x , y ≦ r}
これは、中心を原点に置く半径rの円に外接する正方形(の内部)を表している。
円を同様に表すと、
{ ( x , y ) | sqrt(x2+y2) ≦ r} ※(sqrtは平方根)
となる。「原点からの距離がr以下である(輪郭について言えばrに等しい)」という条件がひとつの式で表せることから、円の場合はx2+y2 = r2 といったスマートな方程式表現が可能になる。
この円の方程式と同様の数式で正方形を記述することも可能である。(x/a)2+(y/b)2 = 1 ( a,b > 0)という楕円の方程式を応用して、
| x/r | p + | y/r | p = 1 ( r >0 , p > 0 )
という式を考えると、p を ∞ に近づけた場合に、半径 r の円に外接する正方形が表現できる。
3.3.正方形の数学的性質と応用
他の正多角形に対し、正方形の基本的な特徴は、
1)縦横、対角線方向に直交(独立)軸をもつこと、2)いずれの軸方向についても対称性があること、3)面(積)の単位として平面を充填できること、などである。
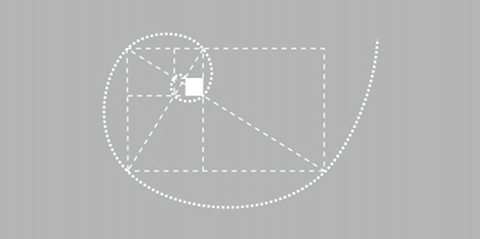
対角線の長さが辺の長さの√2倍になるという特徴も重要である。右図に示すように、辺の長さ1と対角線の長さ√2を直交させれば√3を得ることができ、同様に√3から√4、√5、√6…の長さを順次得ることができる。正方形の面積は(辺の長さ)2であるから、2倍、3倍、4倍…と整数倍の面積をもつ正方形が描けることになる註10)。
正方形はまた、図形的に様々な角度、比率、形状を導き出せる。90度、45度はもちろん、√3倍と2倍の長さを用いることで30度と60度も得られる。比率では、白銀比(1:√2)、黄金比(1:1.618…)、黄金比から対数螺旋など、様々な応用展開が可能である。
3.4.正方形の描画
定規やコンパスといった一般的な製図用具を用いる場合、紙などを折る場合、屋外空間でロープのような道具を用いる場合、さらにソフトウエアの画面上で描画ツールを用いる場合、「正方形を描く」には様々な場合が考えられる。
1) 製図用具による描画
まず、一般的な製図用具で紙に描く場合である。
最も直感的な方法は三角定規を使う方法であろう。例えば小学生に正方形を描く課題を与えると、ほとんどの場合、三角定規の直角部分を使って角をとり、それから縦横の長さを揃えて、それぞれの平行線で正方形を描く。丁寧に行えばこれでも十分だが、角が鈍くなる、不足する長さを延長する際に線がダブる、など作画の美しさに欠ける。
そこで、デザインや製図の現場では、コンパスを用いたスマートな作図が好まれる。
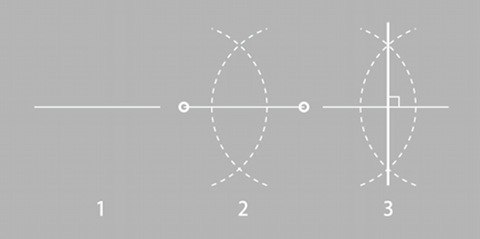
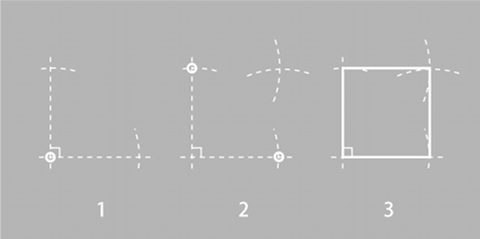
直線定規とコンパスを使う場合、まず直交する2本の線を描くことが必要になる。一般には線分をひとつ描き、コンパスを使って両端から等距離にある2点を求めて、垂直二等分線を描く(右図)。
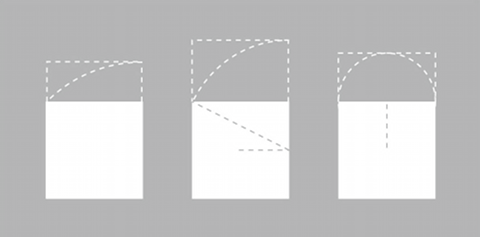
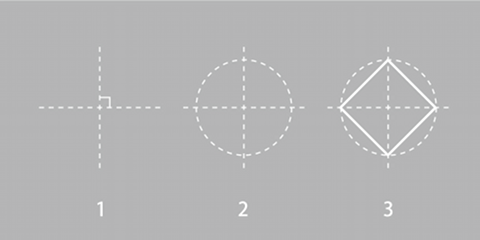
直交する2本の線ができれば、あとは簡単である。下図(左)のように、得られた直角の部分を隅にして同じ長さの辺を順次求めていくか、あるいは下図(右)に示すように交点を中心に円を描けばよい(ただしこの場合は半径の√2倍長の辺をもつ正方形を描くことになる)。
2) 「折り」による描画
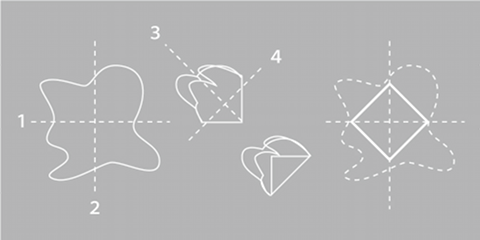
どのような形の紙でも、縦と横に2回折れば、十字(直交する)の折り目ができる。2回折り重ねたまま、その角から斜めに折って45度の折り目をつけ、その折り目と直交するように新たな折り目をつければ、最終的に、はじめの十字の線を対角線とする正方形の折り目ができる。
折り紙の経験がある日本人ならば誰もが思いつく方法だが、任意の形状の平面から、定規もコンパスも必要とせずに形を得ることができるという点で、非常に省資源的なアイデアだといえる。
3) ロープ(ひも)による描画
グラウンドのような広い空間では、とりあえず長いロープが一本あればよい。一ヶ所固定すればコンパスとして、また単位長さの整数倍に目盛を打てば直線定規として使うことができる。つまり、コンパスと定規で紙に描くのと同じことができる。
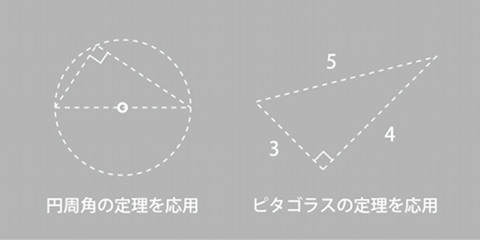
さらにロープの場合、右図に示すような円周角の定理やピタゴラスの定理も簡単に活用できる。円の直径を底辺として、円周上の任意の点で三角形をつくれば、円周角の性質から直角が得られる。また、適当な単位長さに目盛を打ち、3:4:5の比を持つ三角形になるようにロープを張る、という方法でも直角三角形が得られる。この三角形を90度ずつ回転しながら利用すれば、3単位長あるいは4単位長の正方形が得られる。ロープは万能ツールである。
4) ソフトウエアによる描画
一般にドロー系のツール(Inkscape、Illustratorなど)では、矩形ツールを用いる際に[CTRL]あるいは[SHIFT]を押しながらドラッグすると、縦横を等しくする制限が効いて、正方形が描かれる。
またペイント系ツール(TheGIMP、Photoshopなど)の場合も、矩形選択ツールで同様の操作をすれば、正方形の選択領域ができるので、あとはその領域内を塗れば正方形の色面ができる。
いずれも初心者にとっては「最初の難問」となっているのだが、[CTRL]や[SHIFT]がカーソルの動きに制約を与えるという仕組みは、今日多くのソフトウエアで採用されている。
4.様々な正方形
正方形は日常の様々な場面に現れる。ここでは、それらの分類整理に関する試案を示したい。
ムナーリはおそらく百科事典を参考にそのリストアップを行ったものと推察されるが、今日では別の方法がある。それはWebよる記事検索あるいは画像検索である。「9x9」などのキーワードで検索を行うと、項目数が9、寸法が9cm、さらに画像のサイズが9pixelのものなどがヒットする。「1x1」から順に試すと、所々0件となるが、数えられる範囲では必ず何かがヒットする。
ムナーリは、アルファベット順に列挙したが、ここでは便宜的に、空間、プロダクト、ビジュアルと大きく3つの分野に整理を試みた。
4.1.空間デザインおける正方形
等幅の道路が縦横に交わると、その交差点は正方形になる。交差点を含む街区や公園、広場など、スクエアという名が与えられるエリアは文字通り正方形の屋外空間である。また正方形の屋内空間も多い。大半の建材は基本的にユニットで提供されるものであり、空間はおのずとその整数倍になる。正方形の空間はその典型として現れる。
4.2.プロダクトデザインにおける正方形
モノの形に正方形が現れるのには、ふたつの理由がある。ひとつはその目的・用途のために積極的に正方形が採用される場合で、例えばコタツ、将棋やチェスなどのボード、ブロック(LEGO)などがある。もうひとつは外的要因で結果的に正方形が採用されるもので、例えば食器(回転体)を入れる箱、時計(回転する針)の外観などがある。表では「その他」に分類したが、食品における正方形も、製造工程にある器具や、梱包する際の効率の良さにその理由があるといえる。
4.3.ビジュアルデザインにおける正方形
正方形の画素を要素として、縦横に配列される文字やアイコン、円形のレンズに対応する投影面、そして、MAX BILL、VAN DOESBURG、CASIMIR MALEVICH、PIET MONDRIANなどの絵画作品、正方形はビジュアルのフレームとして、造形要素として、また美的構成の原理として、多くの視覚情報の中に現れる。
4.4.自然界の正方形
惑星の軌道から水滴まで、自然界にあるものは円形状に安定するものが多く、立方晶構造をもつ鉱物を除くと、非連続な角のある正方形が自然に出現することは稀である。黄鉄鉱(右図)を見て人工的な印象を受けるのは、正方形自身がもつ高度に抽象的な秩序のせいであろう。
4.5.日本の中の正方形
1)四畳半
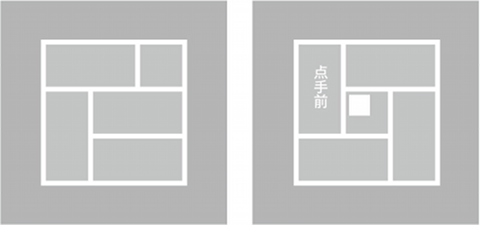
四畳半は畳4枚半で構成された正方形の空間で、茶室に代表される日本家屋の典型的な間取りである。図11に示すように、パズルのごとく様々な敷き詰め方が可能であるが、茶室用には図の右のように、中央に炉を切った四畳半切本勝手といわれる卍形の構成が一般的である。桂離宮の「四つ腰掛」のアイデアと同様、例えば4人がそれぞれ一枚ずつ点対称な位置に座った場合、正面同士で視線がぶつかることがない。狭い空間の中で複数の人間がストレスなく過ごすための知恵がある。
2)畳
畳は、稲藁を圧縮して縫い止めた「畳床」を芯材として、その表面をイグサを編み込んだ「畳表」でくるんだ床材である。大きさは一般に3尺×6尺(910×1820 mm)といわれるが、京間(本間)、中京間(三六間)、江戸間(田舎間)、団地間(公団サイズ)など地域や建造物の規格により大きさは異なる。一般的な畳はダブルスクエアだが、半畳サイズのもの、また琉球畳は正方形である。いずれもレイアウトに関して自由な建材で、その表面が縦横のテクスチュアをもつことで、組合せのバリエーションは豊富である。
3)座布団
江戸時代から普及した調度品。正確には非正方形で、木綿判(51×55 cm)、銘仙判(55×59 cm)、八端判(59×63 cm)などのサイズがある。
日本では客人に対して座布団を裏返して差し出すという慣習がある。客人専用の座布団を別途で作る(さらに管理する)という無駄なことはせず、ひとつの座布団の「使いこなし」によってそれを解決する。客人を不快にさせないためには「座布団を裏返すのが礼儀である」という知識を双方で共有することが前提となるが、表と裏の差がない、すなわち「何もしない」デザインが、資源効率の向上に貢献することを示す好例といえる。
4)風呂敷
風呂敷は、江戸時代以降の銭湯の発達とともに、衣類を包む道具として町人の間に広まったものである。織物の一反を利用して無駄なく裁断・縫製するもので、小幅(約34cm)を基準の一幅として七幅(228cm)までの大きさがある。
岡田(1972)は、「日本人のイメージ構造」の中で、西欧と日本の文化をトランクと風呂敷に例えて述べている。中味のサイズに応じて複数必要になるトランクに対し、風呂敷は「すこぶる直感的に中味の形、容量に順応する」註11)。正方形の布は、一定の「手続き」を経なければただの布であるが、経験者による技の伝授と学習によって、包むということに関して万能のツールとなる。
5)折り紙
折り紙(origami)には、熨斗のような儀礼折り紙と、折り鶴のような遊戯折り紙がある。起源については不明であるが、日本人のほぼ全員がその技術を共有する伝統文化のひとつで、現在教育用には15cm角の正方形の紙が用いられる。
紙を折るということについて特質すべきことは、正方形ではない任意形状の紙であっても、前節で述べたように数回折ることで正方形の折り目を得ることができるという点である。紙を折ることによって、様々な平面形状・立体形状が得られる。紙という造形素材を生活のあらゆる場面で活用してきた日本人独特の知の共有である。
6)つくばい
つくばい(蹲踞)は手を清めるために露地(茶庭)に置かれる器で、自然石を利用したもの、灯篭や塔のパーツを転用して作った「見立てもの」、江戸時代以降の「創作もの」などがある。
正方形は他からの転用が利きやすい。柱を立てるという役割を終えた正方形の窪みは、水を溜めるというアイデアを触発する。資源を消費してモノをつくるのではなく、そこにあるものを活かすという日本的なデザインの発想がある。
5.正方形の特質
5.1.日常の中から
以上のように、我々の身の回りにある様々な正方形をみると、そこから正方形についてのいくつかの知見が見出される。
まず第一に、それが「人間の関与」を感じさせる存在だということである。重力、遠心力、表面張力。自然界では円形状に安定するものが多く、角のあるものは時とともに丸くなる。分子結合・結晶化のように要素が格子状に結びついて安定化する場合を除けば、正方形状のものは、ほぼ間違いなく人間の意志にもとづく秩序構成の結果もたらされたものだと考えることができる。正方形を見たときに、我々が最初に感じ取っていることは、「そこに人間の理性が関与している」ということであろう。出原(2009)によれば、近世の思想家、中村藤樹(1608-1648)も熊沢蕃山(1619-1691)も、理を□で表し、気を○で表すことで、その思想を図的に表現しているという註12)。
第二に、正方形は「分節・秩序」を発生させるということである。正方形を置くと、上下左右という空間の分節が生じる(円は中心を暗示するが、空間の分節は行わない)。点対称、線対称であるという点では正多角形も円も同じであるが、それを単位として空間の充填ができるか、という点で正方形は優れた単位だといえる。我々人間は、正方形を区画単位にすることで、縦と横、東西南北、2軸が直交する世界に住んでいる。
第三に、正方形は様々な秩序の組換え・応用展開に対応できるという点である。ボードゲームやダイスをみれば明らかなように、ひとつのものから展開できるルール(秩序)は複数ある。いわゆる「ワンソース・マルチユース」が可能なのだ。
そして第四に、正方形は「使い手に学習と情報共有を要求する」ということである。畳、座布団、風呂敷、折り紙。それらは初めから「ワンソース・マルチユース」というわけではない。それを使う人間が知識と技術を持ち、同時にそれが共同体の成員間で共有されてはじめて、秩序ある省資源化に寄与するのである。
5.2.造形活動の中から
正方形から様々な角度、比率、平方根などを図的に導きだせることは第3節で触れたが、4つの頂点、辺、対角線、中心を活用すれば、垂直・水平・45度の構成はもちろん、移動・回転・スケーリングといった変換操作の組み合わせで、無限の造形表現が可能になる。イーラム(2005)も強調しているように、造形的な美の大半は、幾何学的な原理によってつくりだすことができる註13)。優れた対称性ゆえに多くの原理を適用することができる正方形は、造形における活用可能性がそれだけ豊富にあるのだ。例えば、既存の作品に対して、その造形的秩序を損なわないように「正方形でトリミングする」また、「画面の中に正方形を書き加える」ということも可能であろう。
では、実際の造形行為において作者が意識するのは正方形のどのような特徴であろうか。筆者は、「正方形のみを図形要素とした平面構成」という実習課題を設定し註14)、履修生に制作上の配慮項目についての聞き取り調査を行った(N=49)。「正方形の特徴を生かす操作」として最も多かったのは「回転(9)」、次いで「重ね・連続(6)」、そして「画素として扱う(3)」(以下略)というものであった。
正方形はその回転によって様々な角度を出せる。ムナーリもいうように「一辺の上に置かれると静的であり、角の上に置かれると動的である」註15)。
単体で緊張と安定の2種の状態を表現できる点で正方形は円よりも表現のバラエティーに富むのだ。緊張と安定の構図。音楽的なモーション。正方形は、時間の流れを肯定する日本人の視覚文化註16)にとっても親和性の高い造形要素だといえる。
6.まとめ
縦と横の道が交わるところにできる広場、布や紙を2回折ることで生まれる直交軸、正方形という形は、人間の理性的な行動を契機に生まれるという点において、「秩序」の起源であるといえる。直交する2つの軸とその対称性は、空間の充填を可能にすると同時に、その秩序構成の最小単位として、全体の計測と再構成を可能にする。
正方形の優れた対称性は、回転や反転といった操作に安定的に対応することで、様々な「変形」や「転用」を可能にする。それは、「ワンソース・マルチユース」なプロダクトの基本原理であり、使い手に様々な「編集の機会」を与える契機となる。正方形は完全な形ではあるが、「生産完成品」としてではなく、編集可能性を秘めた「生産性」としてそこにあるのだ。
使い手には「訓練」が求められる。しかし、物質とエネルギーを使って、個別に複数のモノをつくるより、使い手の知恵と技によってモノの関係を編集するという情報のデザインの方が、時代のニーズに合っているのではないだろうか。用途が限定されたモノは稼働率が低い。もったいない。人を訓練して、ひとつのモノを様々に使いこなす方が、その稼働率ははるかに高くなるのである。
短命な紙、折りたためる布、変形、回転、転用、日本人は「無常」を前提とすることで、正方形による「編集」「再構築」の仕組みをつくりあげてきた。一つの神でも一つの思想でもない、知恵と技の共有によって「和」を成す日本の文化には、その水面下にも正方形をデザインに生かすためのアイデアが数多く存在すように思われる。
空間、モノ、情報。あらゆる場面に正方形は現れる。緊張と安定、いずれも表現し得る正方形は、それ自体、人を触発する仕組みを内包している。資源・エネルギーを使わない問題解決には、作り手も使い手も含めた「知の共有」が前提となるが、その形からは、人と社会を豊かに演出する様々な仕掛けが生み出せるであろう。正方形という形から「編集可能な仕組み」のデザインへ。その提案が今後の課題である。
あとがき
芸術工学とは何か、それはおそらく謎である。しかし、「正方形がデザインにどう生かせるのか」などという収まりのつかない議論を展開するには、「人間に関わる関係諸学の総合」を謳う芸術工学のフィールドが必要である。
大量のエネルギーを消費する科学技術に限界が見えてきた今日、「知の共有を前提とした編集可能な仕組みの提案」という「正方形的な発想」は、ひとつの解決の糸口となるような気がしている。 2008年12月、芸術工学は「哲学」に属する学問として日本学術会議に登録された。
註
1) https://design.kyusan-u.ac.jp/OpenSquareJP
2) Web検索ではx(英小文字)を用いた「9x9」が有効
3) P.クレー(利光功訳),1991,「教育スケッチブック」,バウハウス叢書2,中央公論美術出版
4) W.カンディンスキー(宮島久雄訳),1995,「点と線から面へ」,バウハウス叢書9,中央公論美術出版
5) K.イーラム(伊達尚美訳), 2005, Balance in Design,株BNN新社
6) AGORA:古代ギリシアのポリスにおける広場、市場
7) WANG HSI-CHIH(王羲之):中国晋時代の書美術家
8) PD:Public Domain / CC:Creative Commons
9) 大辞林 第二版,1995,三省堂
10) 参考:A0は1m2、A1は0.5m2…、A4は0.0625m2
11) 岡田晋,1981,日本人のイメージ構造,中公新書
12) 出原立子,2009,近世思想家の図的表現,芸術工学会誌No.51,pp.16-17
13) K.イーラム,前掲書,p.5
14) CG実習I(デザイン学科2年次)で2009年10月実施。対照実験として「円のみを図形要素とした平面構成」という課題も実施した。
15) ブルーノムナーリ(上松正直訳), 1971,正方形-その発見と展開,美術出版社,p.5
16) 井上貢一,1990,『流れ』の研究,映像と理論 Vol.23
図版出典
1) Quadrilateral hierarchy.png BY: Gdr
2) Pyrite…Spain 2.jpg BY:Noodle snacks(www.noodlesnacks.com)
3) Tsukubai.JPG Public Domain